
分析 由題原分式不等式,可通分化簡為標準的分式不等式,因為含有參數a,需根據兩根的大小(有三種情況)進行分類討論而得出相應的解集;最后綜合可得解集.
解答 解:原不等式可化為$\frac{(a+2)x-4}{x-1}-2≤0$,即$\frac{ax-2}{x-1}≤0$.
當$\frac{2}{a}=1$即a=2時,解集為∅;
當$\frac{2}{a}>1$,即0<a<2時,解集為{x|1<x$≤\frac{2}{a}$};
當$\frac{2}{a}<1$,即a<2時,解集為{x|$\frac{2}{a}≤$x<1};
綜上所述0<a<2時,解集為{x|1<x$≤\frac{2}{a}$};
a=2時,解集為∅;
a>2時,解集為{x|$\frac{2}{a}≤$x<1}.
點評 本題考查了分式不等式的解法以及討論的數學思想;關鍵是明確討論的插入點,正確分類.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
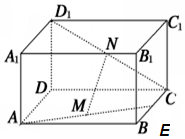 如圖,已知長方體ABCD-A1B1C1D1中,E、M、N分別是BC、AE、CD1的中點,AD=AA1=a,AB=2a.求證:MN∥平面ADD1A1.
如圖,已知長方體ABCD-A1B1C1D1中,E、M、N分別是BC、AE、CD1的中點,AD=AA1=a,AB=2a.求證:MN∥平面ADD1A1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com