
分析 (1)化簡f(x),求得單調區間,由定義證明單調性,注意取值、作差、變形和定符號、下結論;
(2)應用定義,取值、作差、變形和定符號、下結論,即可得到a的取值范圍.
解答 解:(1)當a=1時,$f(x)=1-\frac{2}{x+1}$,在(-∞,-1)上單調遞增,在(-1,+∞)單調遞增,
設x1,x2是區間(-1,+∞)上的任意兩個實數,且x1<x2,則$f({x_1})-f({x_2})=\frac{{2({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}$.
∵x1,x2∈(-1,+∞),且x1<x2,∴x1-x2<0,x1+1>0,x2+1>0,
∴$\frac{{2({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}<0$,
∴f(x1)-f(x2)<0,∴f(x1)<f(x2),
∴函數f(x)在區間(-1,+∞)上單調遞增;
同理,當x1,x2∈(-∞,-1)且x1<x2時,又x1-x2<0,x1+1<0,x2+1<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
所以函數f(x)在(-∞,-1)上單調遞增.
(2)設0<x1<x2,則x1-x2<0,x1+1>0,x2+1>0,
若使f(x)在(0,+∞)上是減函數,只要f(x1)-f(x2)>0,
而$f({x_1})-f({x_2})=\frac{{(a+1)({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}$,
所以當a+1<0,即a<-1時,有f(x1)-f(x2)>0,
所以f(x1)>f(x2),
∴當a<-1時,f(x)在定義域(0,+∞)內是單調減函數,
即所求實數a的取值范圍是(-∞,-1).
點評 本題考查函數的單調性的判斷和證明,以及應用,考查化簡運算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | { 2,3 } | B. | { 1,5,6,7 } | C. | { 6,7 } | D. | { 1,5 } |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
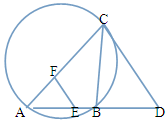 如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD與點D,E,F分別為弦AB,AC上的點,且BC•AE=DC•AF,B,E,F,C四點共圓.
如圖,CD為△ABC外接圓的切線,AB的延長線交直線CD與點D,E,F分別為弦AB,AC上的點,且BC•AE=DC•AF,B,E,F,C四點共圓.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com