
某企業有兩個生產車間,分別位于邊長是 的等邊三角形
的等邊三角形 的頂點
的頂點 處(如圖),現要在邊
處(如圖),現要在邊 上的
上的 點建一倉庫,某工人每天用叉車將生產原料從倉庫運往車間,同時將成品運回倉庫.已知叉車每天要往返
點建一倉庫,某工人每天用叉車將生產原料從倉庫運往車間,同時將成品運回倉庫.已知叉車每天要往返 車間5次,往返
車間5次,往返 車間20次,設叉車每天往返的總路程為
車間20次,設叉車每天往返的總路程為 .(注:往返一次即先從倉庫到車間再由車間返回倉庫)
.(注:往返一次即先從倉庫到車間再由車間返回倉庫)

(Ⅰ)按下列要求確定函數關系式:
①設 長為
長為 ,將
,將 表示成
表示成 的函數關系式;
的函數關系式;
②設 ,將
,將 表示成
表示成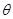 的函數關系式.
的函數關系式.
(Ⅱ)請你選用(Ⅰ)中一個合適的函數關系式,求總路程  的最小值,并指出點
的最小值,并指出點 的位置.
的位置.
(Ⅰ)①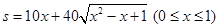 ;②
;②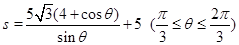 ;
;
(Ⅱ)當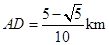 時,總路程
時,總路程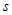 最小,最小值為
最小,最小值為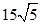
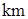 .
.
【解析】
試題分析:(Ⅰ)①是借助余弦定理將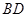 用
用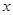 表示出來,然后根據
表示出來,然后根據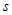 的實際意義利用
的實際意義利用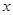 表示出來,但同時也應注意自變量
表示出來,但同時也應注意自變量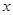 的取值范圍;②借助正弦定理將
的取值范圍;②借助正弦定理將 、
、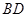 的長度用
的長度用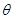 表示出來,然后將
表示出來,然后將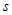 利用以
利用以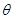 為自變量的函數表示出來,并注意自變量
為自變量的函數表示出來,并注意自變量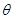 的取值范圍;(Ⅱ)選擇②中的函數解析式,利用導數求極值,從而確定
的取值范圍;(Ⅱ)選擇②中的函數解析式,利用導數求極值,從而確定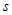 的最小值.
的最小值.
試題解析: (Ⅰ)①在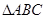 中,
中,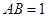 ,
,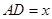 ,
,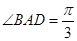 ,
,
由余弦定理,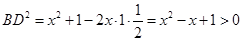 ,
,
所以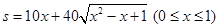 . 3分
. 3分
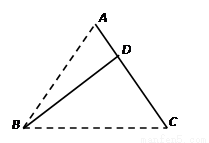
②在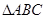 中,
中,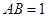 ,
,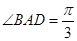 ,
,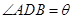 ,
,
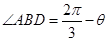 .
.
由正弦定理,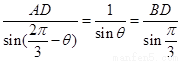 ,
,
得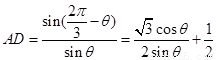 ,
,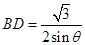 ,
,
則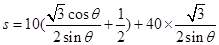
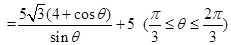 . 6分
. 6分
(Ⅱ)選用(Ⅰ)中的②的函數關系式,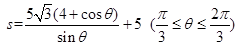 ,
,
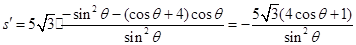 ,
,
由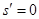 得,
得, ,記
,記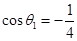 ,
,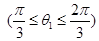
則當 時,
時, ,
,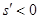 ;當
;當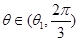 時,
時,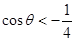 ,
,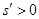 ;
;
所以當 ,時,總路程
,時,總路程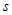 最小值為
最小值為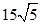 ,
,
此時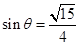 ,
,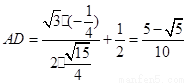 ,
,
答:當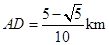 時,總路程
時,總路程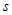 最小,最小值為
最小,最小值為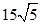
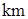 .
13分
.
13分
考點:正弦定理、余弦定理、函數的極值與最值


科目:高中數學 來源: 題型:
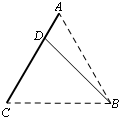 某企業有兩個生產車間分別在A、B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A、B、C中任意兩點間的距離均是1km,設∠BDC=α,所有員工從車間到食堂步行的總路程為S.
某企業有兩個生產車間分別在A、B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A、B、C中任意兩點間的距離均是1km,設∠BDC=α,所有員工從車間到食堂步行的總路程為S.查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南京市白下區高三二模數學試卷 題型:解答題
(本小題滿分15分)
某企業有兩個生產車間分別在A,B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A,B,C中任意兩點間的距離均有1 km,設∠BDC= ,所有員工從車間到食堂步行的總路程為S.
,所有員工從車間到食堂步行的總路程為S.

(1)寫出S關于 的函數表達式,并指出
的函數表達式,并指出 的取值范圍;
的取值范圍;
(2)問食堂D建在距離A多遠時,可使總路程S最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分15分)
某企業有兩個生產車間分別在A,B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A,B,C中任意兩點間的距離均有1 km,設∠BDC=![]() ,所有員工從車間到食堂步行的總路程為S.
,所有員工從車間到食堂步行的總路程為S.
 (1)寫出S關于
(1)寫出S關于![]() 的函數表達式,并指出
的函數表達式,并指出![]() 的取值范圍;
的取值范圍;
(2)問食堂D建在距離A多遠時,可使總路程S最少?
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省蘇州市五市三區高三(上)期中數學試卷(解析版) 題型:解答題
 某企業有兩個生產車間分別在A、B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A、B、C中任意兩點間的距離均是1km,設∠BDC=α,所有員工從車間到食堂步行的總路程為S.
某企業有兩個生產車間分別在A、B兩個位置,A車間有100名員工,B車間有400名員工,現要在公路AC上找一點D,修一條公路BD,并在D處建一個食堂,使得所有員工均在此食堂用餐,已知A、B、C中任意兩點間的距離均是1km,設∠BDC=α,所有員工從車間到食堂步行的總路程為S.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com