
【題目】已知函數![]() ,
,![]() (
(![]() 且
且![]() )
)
(1)判斷函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)當![]() 時,直接寫出函數
時,直接寫出函數![]() 的單調區間(不需證明)
的單調區間(不需證明)
(3)若![]() ,求a的取值范圍.
,求a的取值范圍.
 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】某闖關游戲共有兩關,游戲規則:先闖第一關,當第一關闖過后,才能進入第二關,兩關都闖過,則闖關成功,且每關各有兩次闖關機會.已知闖關者甲第一關每次闖過的概率均為![]() ,第二關每次闖過的概率均為
,第二關每次闖過的概率均為![]() .假設他不放棄每次闖關機會,且每次闖關互不影響.
.假設他不放棄每次闖關機會,且每次闖關互不影響.
(1)求甲恰好闖關3次才闖關成功的概率;
(2)記甲闖關的次數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望.。
的分布列和期望.。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某地區初中升學體育考試規定:考生必須參加長跑、擲實心球、1分鐘跳繩三項測試.某學校在九年級上學期開始,就為掌握全年級學生1分鐘跳繩情況,抽取了100名學生進行測試,得到下面的頻率分布直方圖.
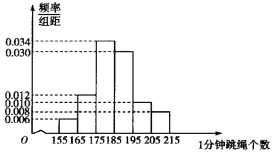
(Ⅰ)規定學生1分鐘跳繩個數大于等于185為優秀.若在抽取的100名學生中,女生共有50人,男生1分鐘跳繩個數大于等于185的有28人.根據已知條件完成下面的![]() 列聯表,并根據這100名學生的測試成績,判斷能否有99%的把握認為學生1分鐘跳繩成績是否優秀與性別有關.
列聯表,并根據這100名學生的測試成績,判斷能否有99%的把握認為學生1分鐘跳繩成績是否優秀與性別有關.
1分鐘跳繩成績 | 優秀 | 不優秀 | 合計 |
男生人數 | 28 | ||
女生人數 | 100 | ||
合計 | 100 |
(Ⅱ)根據往年經驗,該校九年級學生經過訓練,正式測試時每人1分鐘跳繩個數都有明顯進步.假設正式測試時每人1分鐘跳繩個數都比九年級上學期開始時增加10個,全年級恰有2000名學生,若所有學生的1分鐘跳繩個數![]() 服從正態分布
服從正態分布![]() ,用樣本數據的平均值和標準差估計
,用樣本數據的平均值和標準差估計![]() 和
和![]() ,各組數據用中點值代替),估計正式測試時1分鐘跳繩個數大于183的人數(結果四舍五入到整數
,各組數據用中點值代替),估計正式測試時1分鐘跳繩個數大于183的人數(結果四舍五入到整數
附: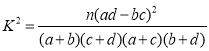 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,各項均不相等的數列
,各項均不相等的數列![]() 滿足
滿足![]()
![]() .令
.令![]() .給出下列三個命題:
.給出下列三個命題:
(1)存在不少于3項的數列![]() ,使得
,使得![]() ;
;
(2)若數列![]() 的通項公式為
的通項公式為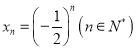 ,則
,則![]() 對
對![]() 恒成立;
恒成立;
(3)若數列![]() 是等差數列,則
是等差數列,則![]() 對
對![]() 恒成立.
恒成立.
其中真命題的序號是( )
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856331)
甲、乙兩家快餐店對某日7個時段的光顧的客人人數進行統計并繪制莖葉圖如下圖所示(下面簡稱甲數據、乙數據),且乙數據的眾數為17,甲數據的平均數比乙數據平均數少2.
(Ⅰ)求a,b的值,并計算乙數據的方差;
(Ⅱ)現從乙數據中不大于16的數據中隨機抽取兩個,求至少有一個數據小于10的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,過點
,過點![]() 的直線與拋物線交于
的直線與拋物線交于![]() 兩點,又過
兩點,又過![]() 兩點分別作拋物線的切線,兩條切線交于
兩點分別作拋物線的切線,兩條切線交于![]() 點。
點。
(1)證明:直線![]() 的斜率之積為定值;
的斜率之積為定值;
(2)求![]() 面積的最小值
面積的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=2sin(ωx+φ)(ω>0,|φ|<![]() )的一個零點為
)的一個零點為![]() ,其圖象距離該零點最近的一條對稱軸為x=
,其圖象距離該零點最近的一條對稱軸為x=![]() .
.
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)若關于x的方程f(x)+log2k=0在x∈[![]() ,
,![]() ]上恒有實數解,求實數k的取值范圍.
]上恒有實數解,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正整數數列中,由1開始依次按如下規則取到的項:第一次取1;第二次取2個連續的偶數2,4;第三次取3個連續的奇數5,7,9:第四次取4個連續的偶數10,12,14,16……按此規律一直取下去,得到一個子數列1,2,4,5,7,9,10,12,14,16…,則在這個子數列中,第2014個數是( )
A.3965B.3966C.3968D.3969
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com