
 :
: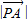 =1:2,
=1:2,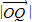 :
: =3:2,連接AQ、BP,設它們交于點R,若
=3:2,連接AQ、BP,設它們交于點R,若 =
= ,
,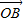 =
= .
. 與
與 表示
表示 ;
; |=1,|
|=1,| |=2,
|=2, 與
與 的夾角
的夾角 ,求
,求 的范圍.
的范圍.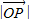 :
: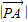 =1:2,點Q在邊OB上且
=1:2,點Q在邊OB上且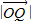 :
: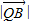 =3:2,我們易將向量
=3:2,我們易將向量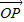 和
和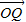 表示成
表示成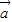 ,
,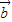 .再根據AQR三點共線,BPR三點共線,我們可以分別得到兩個
.再根據AQR三點共線,BPR三點共線,我們可以分別得到兩個 關于
關于 ,
, 的分解形式,利用平面向量的基本定理,易構造關于λ,μ的方程,進而可用
的分解形式,利用平面向量的基本定理,易構造關于λ,μ的方程,進而可用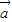 與
與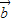 表示
表示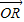 ;
;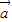 |=1,|
|=1,| |=2,
|=2,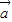 與
與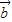 的夾角
的夾角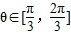 ,結合(I)的結論及RH⊥AB,我們易求出
,結合(I)的結論及RH⊥AB,我們易求出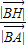 的取值范圍.
的取值范圍.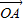 =
=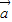 ,點P在邊OA上且
,點P在邊OA上且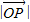 :
: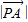 =1:2,
=1:2,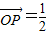 (
(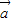 -
-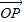 ),
),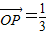
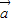 .同理可得
.同理可得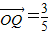
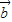 .(2分)
.(2分)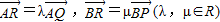 ,
,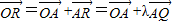 =
=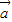 +
+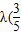
 -
-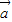 )=(1-λ)
)=(1-λ)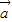 +
+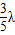
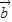 ,
,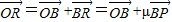 =
= +
+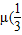
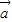 -b)=
-b)=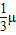
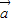 +(1-μ)
+(1-μ)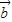 .(4分)
.(4分) 與
與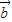 不共線,
不共線,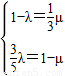 解得
解得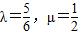
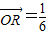
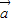 +
+
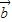 .(5分)
.(5分)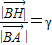 ,則
,則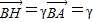 (
(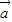 -
-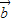 ),
),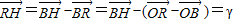 (
(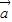 -
-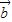 )-(
)-(
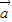 +
+
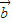 )+
)+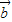 =
=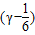
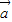 +(
+(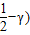
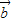 .(6分)
.(6分)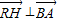 ,
,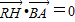 ,
,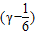
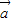 +(
+(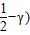
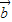 ]•(
]•(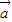 -
-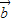 )=0
)=0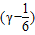
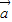 2+(
2+(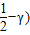
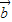 2+
2+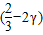
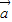 •
•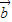 =0(8分)
=0(8分)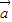 |=1,|
|=1,|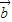 |=2,
|=2,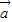 •
•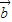 =|
=|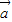 ||
||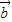 |cosθ=2cosθ,
|cosθ=2cosθ,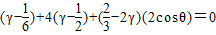
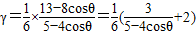 .(10分)
.(10分)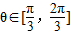 ,
,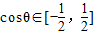 ,
,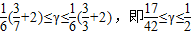 .
.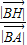 的取值范圍是
的取值范圍是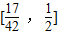 .(12分)
.(12分)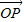 =
=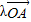 +
+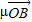 (其中O為直線AB外任一點,且λ+μ=1是解答的關鍵.
(其中O為直線AB外任一點,且λ+μ=1是解答的關鍵. 

科目:高中數學 來源: 題型:
| OP |
| PA |
| OQ |
| QB |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OR |
| a |
| b |
| a |
| b |
| π |
| 3 |
| 2π |
| 3 |
|
| ||
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
在△OAB的邊OA,OB上分別有一點P,Q,已知![]() :
:![]() =1:2,
=1:2, ![]() :
:![]() =3:2,連結AQ,BP,設它們交于點R,若
=3:2,連結AQ,BP,設它們交于點R,若![]() =a,
=a,![]() =b.
=b.
(1)用a與 b表示![]() ;
;
(2)過R作RH⊥AB,垂足為H,若| a|=1, | b|=2, a與 b的夾角![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)在△OAB的邊OA、OB上分別有一點P、Q,已知![]() :
:![]() =1:2,
=1:2, ![]() :
:![]() =3:2,連結AQ、BP,設它們交于點R,若
=3:2,連結AQ、BP,設它們交于點R,若![]() =a,
=a,![]() =b. (Ⅰ)用a與 b表示
=b. (Ⅰ)用a與 b表示![]() ;
;
(Ⅱ)過R作RH⊥AB,垂足為H,若| a|=1, | b|=2, a與 b的夾角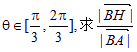 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| OP |
| PA |
| OQ |
| QB |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OR |
| a |
| b |
| a |
| b |
| π |
| 3 |
| 2π |
| 3 |
|
| ||
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com