
【題目】已知函數![]() ,且
,且![]() 的解集為
的解集為![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意
,對任意![]() ,都有
,都有![]()
(1)求數列![]() 的通項公式.
的通項公式.
(2)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
(3)已知數列![]() ,滿足
,滿足 ,若
,若 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根據根與系數的關系求出![]() ,和
,和![]() ,再利用
,再利用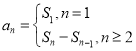 即可求出數列
即可求出數列![]() 的通項公式;
的通項公式;
(2)根據![]() ,
,![]() ,可證明
,可證明![]() 為等比數列,求得
為等比數列,求得![]() ,
,![]() ,再根據錯位相減法即可求出結果;
,再根據錯位相減法即可求出結果;
(3)由題意可知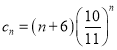 ,可得
,可得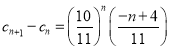 ,易知當
,易知當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,當
,當![]() 時,
時, ![]() ,進而求出有
,進而求出有![]() 的最大值為
的最大值為![]() ,再根據不等式恒成立可列出不等式,解不等式,即可求出結果.
,再根據不等式恒成立可列出不等式,解不等式,即可求出結果.
(1)![]() 的解集為
的解集為![]() ,∴
,∴![]() 是方程
是方程![]() 的兩根
的兩根
由韋達定理知![]() ,解得
,解得![]() ,∴
,∴![]() ,得
,得![]()
當![]() 時,有
時,有![]()
當![]() 時,有
時,有![]()
![]() 也符合
也符合![]() ,∴
,∴![]()
(2)當![]() 時,有
時,有![]() ,即
,即![]() ,得
,得![]()
當![]() 時,有
時,有![]() ,可得
,可得![]() ,即
,即![]() ,
,
∴![]() 為等比數列,首項為
為等比數列,首項為![]() ,公比為2,
,公比為2,
∴![]() ,∴
,∴![]() .
.
![]() ①,
①,
① ![]() 得,
得,![]() ②
②
①-②得![]()
∴![]()
(3)由題意可知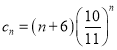 ,
,
則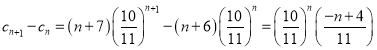
∴當![]() 時,
時,![]() ,即
,即![]()
當![]() 時,
時,![]() ,即
,即![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() ,故有
,故有![]() 的最大值為
的最大值為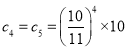
由于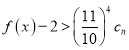 對任意
對任意![]() 恒成立
恒成立
則應有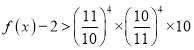 ,
,![]() 或
或![]()
綜上:![]() 的取值范圍是:
的取值范圍是:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】規定:在桌面上,用母球擊打目標球,使目標球運動,球的位置是指球心的位置,我們說球 A 是指該球的球心點 A.兩球碰撞后,目標球在兩球的球心所確定的直線上運動,目標球的運動方向是指目標球被母球擊打時,母球球心所指向目標球球心的方向.所有的球都簡化為平面上半徑為 1 的圓,且母球與目標球有公共點時,目標球就開始運動,在桌面上建立平面直角坐標系,解決下列問題:

(1) 如圖,設母球 A 的位置為 (0, 0),目標球 B 的位置為 (4, 0),要使目標球 B 向 C(8, -4) 處運動,求母球 A 球心運動的直線方程;
(2)如圖,若母球 A 的位置為 (0, -2),目標球 B 的位置為 (4, 0),能否讓母球 A 擊打目標 B 球后,使目標 B 球向 (8,-4) 處運動?
(3)若 A 的位置為 (0,a) 時,使得母球 A 擊打目標球 B 時,目標球 B(4![]() , 0) 運動方向可以碰到目標球 C(7
, 0) 運動方向可以碰到目標球 C(7![]() ,-5
,-5![]() ),求 a 的最小值(只需要寫出結果即可)
),求 a 的最小值(只需要寫出結果即可)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某電視娛樂節目的游戲活動中,每人需完成A、B、C三個項目.已知選手甲完成A、B、C三個項目的概率分別為![]() 、
、![]() 、
、![]() .每個項目之間相互獨立.
.每個項目之間相互獨立.
(1)選手甲對A、B、C三個項目各做一次,求甲至少完成一個項目的概率.
(2)該活動要求項目A、B 各做兩次,項目C做三次.若兩次項目A均完成,則進行項目B,并獲得積分a;兩次項目B均完成,則進行項目C,并獲積分3a;三次項目C只要兩次成功,則該選手闖關成功并獲積分6a(積分不累計),且每個項目之間互相獨立.用X表示選手甲所獲積分的數值,寫出X的分布列并求數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的方程為
的方程為![]() ,以
,以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,取相同的長度單位建立極坐標系,直線
軸非負半軸為極軸,取相同的長度單位建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程和橢圓
的直角坐標方程和橢圓![]() 的參數方程;
的參數方程;
(2)設![]() 為橢圓
為橢圓![]() 上任意一點,求
上任意一點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將2、3、4、6、8、9、12、15共八個數排成一行,使得任意相鄰兩個數的最大公約數均大于1.則所有可能的排法共有()種
A. 720 B. 1014 C. 576 D. 1296
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某體育公司對最近6個月內的市場占有率進行了統計,結果如表:

(1)可用線性回歸模型擬合![]() 與
與![]() 之間的關系嗎?如果能,請求出
之間的關系嗎?如果能,請求出![]() 關于
關于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)公司決定再采購![]() ,
,![]() 兩款車擴大市場,
兩款車擴大市場,![]() ,
,![]() 兩款車各100輛的資料如表:
兩款車各100輛的資料如表:

平均每輛車每年可為公司帶來收入500元,不考慮采購成本之外的其他成本,假設每輛車的使用壽命都是整數年,用每輛車使用壽命的頻率作為概率,以每輛車產生利潤的期望值作為決策依據,應選擇采購哪款車型?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數 ;
;
回歸直線方程![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com