
���}Ŀ����֪���タ![]() �cֱ��
�cֱ��![]() ֻ��һ�������c(di��n)���c(di��n)
ֻ��һ�������c(di��n)���c(di��n)![]() �ǒ��タ
�ǒ��タ![]() �ϵĄ��c(di��n).
�ϵĄ��c(di��n).
��1�����タ![]() �ķ��̣�
�ķ��̣�
��2������![]() �����C��ֱ��
�����C��ֱ��![]() �^���c(di��n)��
�^���c(di��n)��
����![]() �ǒ��タ
�ǒ��タ![]() ���cԭ�c(di��n)���غϵĶ��c(di��n)����
���cԭ�c(di��n)���غϵĶ��c(di��n)����![]() �����C��ֱ��
�����C��ֱ��![]() ��б�ʞ鶨ֵ�������ԓ��ֵ.
��б�ʞ鶨ֵ�������ԓ��ֵ.
���𰸡���1��![]() ��2�����C��Ҋ�������C��Ҋ������
��2�����C��Ҋ�������C��Ҋ������![]()
��������
��1��(li��n)�����タ�cֱ������,�ٸ���(j��)����ֻ��һ�����c(di��n)�ɵ�![]() ,������⣻
,������⣻
��2�����O(sh��) ,
, ,��ֱ��б�ʹ�ʽ����
,��ֱ��б�ʹ�ʽ����![]() �ɵ�
�ɵ�![]() ,��ֱ����б�ʹ�ʽ�ɵ�
,��ֱ����б�ʹ�ʽ�ɵ�![]() ,�M(j��n)����
,�M(j��n)����![]() ����ֱ��
����ֱ��![]() �ķ���
�ķ���![]() ,��������⣻���O(sh��)
,��������⣻���O(sh��) ,
, ,����ֱ��б�ʹ�ʽ����
,����ֱ��б�ʹ�ʽ����![]() �л����ɵ�
�л����ɵ�![]() ,��
,��![]() ,�ٸ���(j��)ֱ��б�ʹ�ʽ��⼴��.
,�ٸ���(j��)ֱ��б�ʹ�ʽ��⼴��.
��:��1��![]() �c
�c![]() (li��n)����
(li��n)����![]() ,
,
��?y��n)钁�タ![]() �cֱ��
�cֱ��![]() ֻ��һ�������c(di��n),
ֻ��һ�������c(di��n),
����![]() ,��
,��![]() ,
,
���Ԓ��タ![]() �ķ��̞�
�ķ��̞�![]() .
.
��2�����C��:�O(sh��) ,
, ,�t
,�t![]() ,
,
����![]() ,��
,�� ,
,
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() ,
,
��![]() ,
,
��(d��ng)![]() �r
�r![]() ,����ֱ��
,����ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() .
.
���C��:�O(sh��) ,
, ,
,
�t ,
,
��![]() ,
,
����![]() ,�t
,�t![]() ,
,
����ֱ��![]() ��б�ʞ�
��б�ʞ� ,
,
��?y��n)?/span>![]() �鶨�c(di��n),
�鶨�c(di��n),
����ֱ��![]() ��б�ʞ鶨ֵ
��б�ʞ鶨ֵ![]() .
.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��![]() ��
��
��1����(d��ng)![]() �r����(sh��)
�r����(sh��)![]() ��
��![]() �ϵ���Сֵ��
�ϵ���Сֵ��
��2��������(sh��)![]() ��
��![]() �ϴ������c(di��n)���C����
�ϴ������c(di��n)���C����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1����֪��߅![]() ��߅�L��3���c(di��n)
��߅�L��3���c(di��n)![]() ��
��![]() �քe��߅
�քe��߅![]() ��
��![]() �ϵ��c(di��n)����
�ϵ��c(di��n)����![]() ��
��![]() .��D2����
.��D2����![]() ��
��![]() ����
����![]() ���.
���.
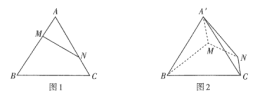
��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���o�������l������![]() ���ڶ����
���ڶ����![]() ��С��
����![]() ����
����![]() .���@�����l�������xһ�����a(b��)�������憖�}�ėl���У��������ھ���
.���@�����l�������xһ�����a(b��)�������憖�}�ėl���У��������ھ���![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹֱ��
��ʹֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() �������ڣ����
�������ڣ����![]() ���L���������ڣ�Ո�f������.ע����������l���քe��𣬰���һ�����o��
���L���������ڣ�Ո�f������.ע����������l���քe��𣬰���һ�����o��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x����|x|+|x��1|��
��1����f��x����|m��1|���������(sh��)��(sh��)m�����ֵM��
��2���ڣ�1�������ėl���£�����(sh��)��(sh��)a��b�M��a2+b2��M���C����a+b��2ab��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����ABC߅�L��3���c(di��n)M��N�քe��AB��AC߅�ϵ��c(di��n)��AN��BM��1����D1��ʾ������AMN��MN����PMN��λ�ã�ʹ����PC�L��![]() ���B��PB����D2��ʾ��
���B��PB����D2��ʾ��
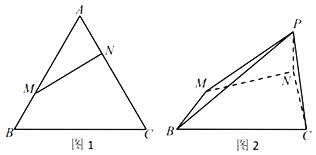
�������C��ƽ��PMN��ƽ��BCNM��
�������c(di��n)D�ھ���BC�ϣ���BD��2DC��������M��PD��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����![]() �����C��
�����C��![]() ..
..
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��������![]() ������
������![]() ���������
���������![]() ��
��![]() ����(c��)��
����(c��)��![]() ����
����![]() .
.
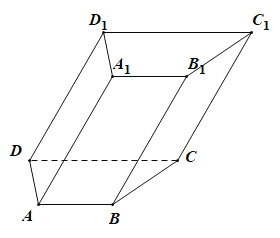
��1���ڂ�(c��)��![]() ���ܷ���һ�lֱ��ʹ���c
���ܷ���һ�lֱ��ʹ���c![]() ƽ�У�����ܣ�Ո�������D�^�̲��o���C����������ܣ�Ո�f�����ɣ�
ƽ�У�����ܣ�Ո�������D�^�̲��o���C����������ܣ�Ո�f�����ɣ�
��2���������w![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������F![]() �У�
�У�![]() .
.
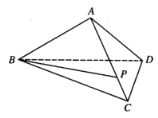
��1�����C��![]() ��
��
��2�����c(di��n)![]() ��
��![]() ��һ�c(di��n)����
��һ�c(di��n)����![]() ����ֱ��
����ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǵ�����ֵ.
���ɵĽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() ��
��![]() ������Ȼ����(sh��)�ĵה�(sh��).
������Ȼ����(sh��)�ĵה�(sh��).
��1��������![]() ���c(di��n)
���c(di��n)![]() ̎���о���
̎���о���![]() ����
����![]() ��ֵ��
��ֵ��
��2����(sh��)![]() �ĘO��ֵ��
�ĘO��ֵ��
��3���O(sh��)����(sh��)![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com