
【題目】![]() 年上半年,隨著新冠肺炎疫情在全球蔓延,全球超過
年上半年,隨著新冠肺炎疫情在全球蔓延,全球超過![]() 個國家或地區(qū)宣布進人緊急狀態(tài),部分國家或地區(qū)直接宣布“封國”或“封城”,隨著國外部分活動進入停擺,全球經(jīng)濟缺乏活力,一些企業(yè)開始倒閉,下表為
個國家或地區(qū)宣布進人緊急狀態(tài),部分國家或地區(qū)直接宣布“封國”或“封城”,隨著國外部分活動進入停擺,全球經(jīng)濟缺乏活力,一些企業(yè)開始倒閉,下表為![]() 年第一季度企業(yè)成立年限與倒閉分布情況統(tǒng)計表:
年第一季度企業(yè)成立年限與倒閉分布情況統(tǒng)計表:
企業(yè)成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企業(yè)成立年限 | 1 | 2 | 3 | 4 | 5 |
倒閉企業(yè)數(shù)量(萬家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒閉企業(yè)所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根據(jù)上表,給出兩種回歸模型:
模型①:建立曲線型回歸模型![]() ,求得回歸方程為
,求得回歸方程為![]() ;
;
模型②:建立線性回歸模型![]() .
.
(1)根據(jù)所給的統(tǒng)計量,求模型②中![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)根據(jù)下列表格中的數(shù)據(jù),比較兩種模型的相關(guān)指數(shù)![]() ,并選擇擬合精度更高、更可靠的模型,預(yù)測
,并選擇擬合精度更高、更可靠的模型,預(yù)測![]() 年成立的企業(yè)中倒閉企業(yè)所占比例(結(jié)果保留整數(shù)).
年成立的企業(yè)中倒閉企業(yè)所占比例(結(jié)果保留整數(shù)).
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
|
|
參考公式: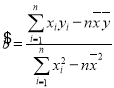 ,
,![]() ;
;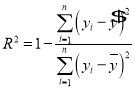 .
.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
 應(yīng)用題天天練四川大學出版社系列答案
應(yīng)用題天天練四川大學出版社系列答案科目:高中數(shù)學 來源: 題型:
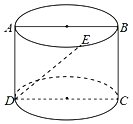
【題目】我們打印用的A4紙的長與寬的比約為![]() ,之所以是這個比值,是因為把紙張對折,得到的新紙的長與寬之比仍約為
,之所以是這個比值,是因為把紙張對折,得到的新紙的長與寬之比仍約為![]() ,紙張的形狀不變.已知圓柱的母線長小于底面圓的直徑長(如圖所示),它的軸截面ABCD為一張A4紙,若點E為上底面圓上弧AB的中點,則異面直線DE與AB所成的角約為( )
,紙張的形狀不變.已知圓柱的母線長小于底面圓的直徑長(如圖所示),它的軸截面ABCD為一張A4紙,若點E為上底面圓上弧AB的中點,則異面直線DE與AB所成的角約為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 是
是![]() 的導(dǎo)函數(shù),討論
的導(dǎo)函數(shù),討論![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() (
(![]() 是自然對數(shù)的底數(shù)),求證:
是自然對數(shù)的底數(shù)),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在疫情這一特殊時期,教育行政部門部署了“停課不停學”的行動,全力幫助學生在線學習.復(fù)課后進行了摸底考試,某校數(shù)學教師為了調(diào)查高三學生這次摸底考試的數(shù)學成績與在線學習數(shù)學時長之間的相關(guān)關(guān)系,對在校高三學生隨機抽取45名進行調(diào)查.知道其中有25人每天在線學習數(shù)學的時長是不超過1小時的,得到了如下的等高條形圖:
(1)是否有![]() 的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關(guān)”;
的把握認為“高三學生的這次摸底考試數(shù)學成績與其在線學習時長有關(guān)”;
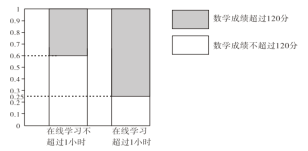
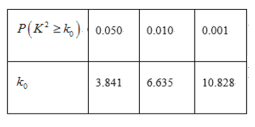
(2)將頻率視為概率,從全校高三學生這次數(shù)學成績超過120分的學生中隨機抽取10人,求抽取的10人中每天在線學習時長超過1小時的人數(shù)的數(shù)學期望與方差.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 與拋物線
與拋物線![]() 有共同的焦點
有共同的焦點![]() ,且兩曲線的公共點到
,且兩曲線的公共點到![]() 的距離是它到直線
的距離是它到直線![]() (點
(點![]() 在此直線右側(cè))的距離的一半.
在此直線右側(cè))的距離的一半.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為坐標原點,直線
為坐標原點,直線![]() 過點
過點![]() 且與橢圓交于
且與橢圓交于![]() 兩點,以
兩點,以![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() .是否存在直線
.是否存在直線![]() ,使點
,使點![]() 落在橢圓
落在橢圓![]() 或拋物線
或拋物線![]() 上?若存在,求出點
上?若存在,求出點![]() 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 不過原點
不過原點![]() 且不平行于坐標軸,
且不平行于坐標軸,![]() 與
與![]() 有兩個交點
有兩個交點![]() ,
,![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(1)若![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 、
、![]() 分別為橢圓的兩個焦點,求
分別為橢圓的兩個焦點,求![]() 的范圍;
的范圍;
(2)若![]() 過點
過點![]() ,射線
,射線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,四邊形
,四邊形![]() 能否為平行四邊形?若能,求此時直線
能否為平行四邊形?若能,求此時直線![]() 斜率;若不能,說明理由.
斜率;若不能,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點
的中點![]() 是由
是由![]() 繞直線
繞直線![]() 旋轉(zhuǎn)得到,連結(jié)
旋轉(zhuǎn)得到,連結(jié)![]() ,
,![]() ,
,![]() .
.
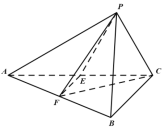
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com