
【題目】已知![]() ,直線
,直線![]() 不過原點(diǎn)
不過原點(diǎn)![]() 且不平行于坐標(biāo)軸,
且不平行于坐標(biāo)軸,![]() 與
與![]() 有兩個(gè)交點(diǎn)
有兩個(gè)交點(diǎn)![]() ,
,![]() ,線段
,線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() .
.
(1)若![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上,
上,![]() 、
、![]() 分別為橢圓的兩個(gè)焦點(diǎn),求
分別為橢圓的兩個(gè)焦點(diǎn),求![]() 的范圍;
的范圍;
(2)若![]() 過點(diǎn)
過點(diǎn)![]() ,射線
,射線![]() 與橢圓
與橢圓![]() 交于點(diǎn)
交于點(diǎn)![]() ,四邊形
,四邊形![]() 能否為平行四邊形?若能,求此時(shí)直線
能否為平行四邊形?若能,求此時(shí)直線![]() 斜率;若不能,說明理由.
斜率;若不能,說明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求得焦點(diǎn)坐標(biāo),設(shè)![]() ,運(yùn)用向量數(shù)量積的坐標(biāo)表示,結(jié)合橢圓的范圍,可得所求范圍;
,運(yùn)用向量數(shù)量積的坐標(biāo)表示,結(jié)合橢圓的范圍,可得所求范圍;
(2)設(shè)![]() ,
,![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]() ,
,![]() ,
,![]() ,運(yùn)用中點(diǎn)坐標(biāo)公式和點(diǎn)差法,直線的斜率公式,結(jié)合平行四邊形的性質(zhì),即可得到所求斜率.
,運(yùn)用中點(diǎn)坐標(biāo)公式和點(diǎn)差法,直線的斜率公式,結(jié)合平行四邊形的性質(zhì),即可得到所求斜率.
解:(1)![]() 時(shí),橢圓
時(shí),橢圓![]() ,兩個(gè)焦點(diǎn)
,兩個(gè)焦點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設(shè)![]() ,可得
,可得![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
因?yàn)?/span>![]() ,
,
所以![]() 的范圍是
的范圍是![]() ;
;
(2)設(shè)![]() ,
,![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
則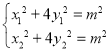 ,兩式相減可得
,兩式相減可得![]() ,
,
![]() ,即
,即![]() ,
,
故![]() ,又設(shè)
,又設(shè)![]() ,
,![]() ,直線
,直線![]() ,
,
即直線![]() 的方程為
的方程為![]() ,
,
從而![]() ,代入橢圓方程可得,
,代入橢圓方程可得,![]() ,
,
由![]() 與
與![]() ,聯(lián)立得
,聯(lián)立得![]() ,
,
若四邊形![]() 為平行四邊形,那么
為平行四邊形,那么![]() 也是
也是![]() 的中點(diǎn),
的中點(diǎn),
所以![]() ,即
,即![]() ,整理可得
,整理可得![]() ,
,
解得![]() ,經(jīng)檢驗(yàn)滿足題意,
,經(jīng)檢驗(yàn)滿足題意,
所以當(dāng)![]() 時(shí),四邊形
時(shí),四邊形![]() 為平行四邊形.
為平行四邊形.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】法國數(shù)學(xué)家龐加是個(gè)喜歡吃面包的人,他每天都會(huì)購買一個(gè)面包,面包師聲稱自己出售的每個(gè)面包的平均質(zhì)量是1000![]() ,上下浮動(dòng)不超過50
,上下浮動(dòng)不超過50![]() .這句話用數(shù)學(xué)語言來表達(dá)就是:每個(gè)面包的質(zhì)量服從期望為1000
.這句話用數(shù)學(xué)語言來表達(dá)就是:每個(gè)面包的質(zhì)量服從期望為1000![]() ,標(biāo)準(zhǔn)差為50
,標(biāo)準(zhǔn)差為50![]() 的正態(tài)分布.
的正態(tài)分布.
(1)假設(shè)面包師的說法是真實(shí)的,從面包師出售的面包中任取兩個(gè),記取出的兩個(gè)面包中質(zhì)量大于1000![]() 的個(gè)數(shù)為
的個(gè)數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(2)作為一個(gè)善于思考的數(shù)學(xué)家,龐加萊每天都會(huì)將買來的面包稱重并記錄,25天后,得到數(shù)據(jù)如下表,經(jīng)計(jì)算25個(gè)面包總質(zhì)量為24468![]() .龐加萊購買的25個(gè)面包質(zhì)量的統(tǒng)計(jì)數(shù)據(jù)(單位:
.龐加萊購買的25個(gè)面包質(zhì)量的統(tǒng)計(jì)數(shù)據(jù)(單位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
盡管上述數(shù)據(jù)都落在![]() 上,但龐加菜還是認(rèn)為面包師撒謊,根據(jù)所附信息,從概率角度說明理由
上,但龐加菜還是認(rèn)為面包師撒謊,根據(jù)所附信息,從概率角度說明理由
附:
①若![]() ,從X的取值中隨機(jī)抽取25個(gè)數(shù)據(jù),記這25個(gè)數(shù)據(jù)的平均值為Y,則由統(tǒng)計(jì)學(xué)知識(shí)可知:隨機(jī)變量
,從X的取值中隨機(jī)抽取25個(gè)數(shù)據(jù),記這25個(gè)數(shù)據(jù)的平均值為Y,則由統(tǒng)計(jì)學(xué)知識(shí)可知:隨機(jī)變量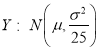
②若![]() ,則
,則![]() ,
,![]() ,
,![]() ;
;
③通常把發(fā)生概率在0.05以下的事件稱為小概率事件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 年上半年,隨著新冠肺炎疫情在全球蔓延,全球超過
年上半年,隨著新冠肺炎疫情在全球蔓延,全球超過![]() 個(gè)國家或地區(qū)宣布進(jìn)人緊急狀態(tài),部分國家或地區(qū)直接宣布“封國”或“封城”,隨著國外部分活動(dòng)進(jìn)入停擺,全球經(jīng)濟(jì)缺乏活力,一些企業(yè)開始倒閉,下表為
個(gè)國家或地區(qū)宣布進(jìn)人緊急狀態(tài),部分國家或地區(qū)直接宣布“封國”或“封城”,隨著國外部分活動(dòng)進(jìn)入停擺,全球經(jīng)濟(jì)缺乏活力,一些企業(yè)開始倒閉,下表為![]() 年第一季度企業(yè)成立年限與倒閉分布情況統(tǒng)計(jì)表:
年第一季度企業(yè)成立年限與倒閉分布情況統(tǒng)計(jì)表:
企業(yè)成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企業(yè)成立年限 | 1 | 2 | 3 | 4 | 5 |
倒閉企業(yè)數(shù)量(萬家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒閉企業(yè)所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根據(jù)上表,給出兩種回歸模型:
模型①:建立曲線型回歸模型![]() ,求得回歸方程為
,求得回歸方程為![]() ;
;
模型②:建立線性回歸模型![]() .
.
(1)根據(jù)所給的統(tǒng)計(jì)量,求模型②中![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)根據(jù)下列表格中的數(shù)據(jù),比較兩種模型的相關(guān)指數(shù)![]() ,并選擇擬合精度更高、更可靠的模型,預(yù)測(cè)
,并選擇擬合精度更高、更可靠的模型,預(yù)測(cè)![]() 年成立的企業(yè)中倒閉企業(yè)所占比例(結(jié)果保留整數(shù)).
年成立的企業(yè)中倒閉企業(yè)所占比例(結(jié)果保留整數(shù)).
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
|
|
參考公式: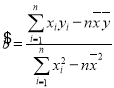 ,
,![]() ;
;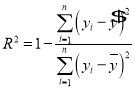 .
.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的兩個(gè)焦點(diǎn)分別是
的兩個(gè)焦點(diǎn)分別是![]() ,直線
,直線![]() :
:![]() 與橢圓交于
與橢圓交于![]() 兩點(diǎn).
兩點(diǎn).
(1)若![]() 為橢圓短軸上的一個(gè)頂點(diǎn),且
為橢圓短軸上的一個(gè)頂點(diǎn),且![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求證:
,求證:![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為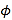 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程和
的普通方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,點(diǎn)
,點(diǎn)![]() 是曲線
是曲線![]() 與
與![]() 的交點(diǎn),點(diǎn)
的交點(diǎn),點(diǎn)![]() 是曲線
是曲線![]() 與
與![]() 的交點(diǎn),
的交點(diǎn),![]() 、
、![]() 均異于原點(diǎn)
均異于原點(diǎn)![]() ,且
,且![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】BMI指數(shù)(身體質(zhì)量指數(shù),英文為BodyMassIndex,簡(jiǎn)稱BMI)是衡量人體胖瘦程度的一個(gè)標(biāo)準(zhǔn),BMI=體重(kg)/身高(m)的平方.根據(jù)中國肥胖問題工作組標(biāo)準(zhǔn),當(dāng)BMI≥28時(shí)為肥胖.某地區(qū)隨機(jī)調(diào)查了1200名35歲以上成人的身體健康狀況,其中有200名高血壓患者,被調(diào)查者的頻率分布直方圖如下:
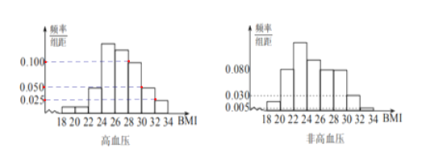
(1)求被調(diào)查者中肥胖人群的BMI平均值![]() ;
;
(2)填寫下面列聯(lián)表,并判斷是否有99.9%的把握認(rèn)為35歲以上成人患高血壓與肥胖有關(guān).
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合計(jì) | |
高血壓 | |||
非高血壓 | |||
合計(jì) |
附: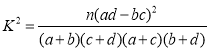 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,斜率為
,斜率為![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點(diǎn),當(dāng)直線
兩點(diǎn),當(dāng)直線![]() 過點(diǎn)
過點(diǎn)![]() 時(shí),以
時(shí),以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 相切.
相切.
(1)求拋物線![]() 的方程;
的方程;
(2)與![]() 平行的直線
平行的直線![]() 交拋物線于
交拋物線于![]() ,
,![]() 兩點(diǎn),若平行線
兩點(diǎn),若平行線![]() ,
,![]() 之間的距離為
之間的距離為![]() ,且
,且![]() 的面積是
的面積是![]() 面積的
面積的![]() 倍(O為坐標(biāo)原點(diǎn)),求
倍(O為坐標(biāo)原點(diǎn)),求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A、B分別為橢圓E:![]() (a>1)的左、右頂點(diǎn),G為E的上頂點(diǎn),
(a>1)的左、右頂點(diǎn),G為E的上頂點(diǎn),![]() ,P為直線x=6上的動(dòng)點(diǎn),PA與E的另一交點(diǎn)為C,PB與E的另一交點(diǎn)為D.
,P為直線x=6上的動(dòng)點(diǎn),PA與E的另一交點(diǎn)為C,PB與E的另一交點(diǎn)為D.
(1)求E的方程;
(2)證明:直線CD過定點(diǎn).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com