
【題目】已知![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 是拋物線上一點,且
是拋物線上一點,且![]() .
.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)過點![]() 的動直線
的動直線![]() 交拋物線于
交拋物線于![]() 兩點,拋物線上是否存在一個定點
兩點,拋物線上是否存在一個定點![]() ,使得以弦
,使得以弦![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)存在點
;(2)存在點![]() 符合題意.
符合題意.
【解析】
(1)利用拋物線上的點到焦點的距離與到到準線的距離相等即可求出![]() 的值,即可求出拋物線方程.
的值,即可求出拋物線方程.
(2)假設存在滿足條件的點,依題設過點![]() 直線的直線的方程為
直線的直線的方程為![]() ,設
,設![]() ,聯立方程由根與系數的關系可得
,聯立方程由根與系數的關系可得![]() ;依題可得
;依題可得![]() ,若能得出關于
,若能得出關于![]() 的成立的恒等式,則滿足條件的點存在,否則就不存在.
的成立的恒等式,則滿足條件的點存在,否則就不存在.
(1)拋物線![]() 的準線方程為
的準線方程為![]() ,
,
所以點![]() 到準線的距離為
到準線的距離為![]() ,又
,又![]() ,
,
由拋物線的定義可得![]() ,所以
,所以![]() ,
,
所以拋物線的方程為:![]() .
.
(2)假設存在點![]() 使以弦
使以弦![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ,
,
設過點![]() 直線的直線
直線的直線![]() 的方程為
的方程為![]() ,
,
聯立方程![]() 得
得![]() ,
,
設![]() ,則
,則![]() ,
,![]() ;
;
因為點![]() 總是在以弦
總是在以弦![]() 為直徑的圓上,
為直徑的圓上,
所以![]() ,所以
,所以![]()
由![]() ,
,![]()
所以![]()
即![]()
當![]() 或
或![]() ,等式顯然成立;
,等式顯然成立;
當![]() 或
或![]() 時,則有
時,則有![]()
即![]() ,則
,則![]() ,
,
即![]()
所以當![]() 時,無論
時,無論![]() 取何值等式都成立,
取何值等式都成立,
將![]() 代入
代入![]() 得
得![]() ,
,
所以存在點![]() 使以弦
使以弦![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】湖北省第二屆(荊州)園林博覽會于2019年9月28日至11月28日在荊州園博園舉辦,本屆園林博覽會以“輝煌荊楚,生態園博”為主題,展示荊州生態之美,文化之韻,吸引更多優秀企業來荊投資,從而促進荊州經濟快速發展.在此次博覽會期間,某公司帶來了一種智能設備供采購商洽談采購,并決定大量投放荊州市場.已知該種設備年固定研發成本為50萬元,每生產一臺需另投入80元,設該公司一年內生產該設備![]() 萬臺且全部售完,每萬臺的銷售收入
萬臺且全部售完,每萬臺的銷售收入![]() (萬元)與年產量
(萬元)與年產量![]() (萬臺)滿足如下關系式:
(萬臺)滿足如下關系式: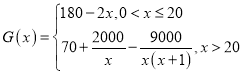 .
.
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (萬臺)的函數解析式;(利潤=銷售收入-成本)
(萬臺)的函數解析式;(利潤=銷售收入-成本)
(2)當年產量為多少萬臺時,該公司獲得的年利潤最大?并求最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,點M、N分別在AB1、BC1上,且AM=![]() AB1,BN=
AB1,BN=![]() BC1,則下列結論:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
BC1,則下列結論:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
正確命題的個數是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,由半圓![]() 和部分拋物線
和部分拋物線![]() 合成的曲線
合成的曲線![]() 稱為“羽毛球開線”,曲線
稱為“羽毛球開線”,曲線![]() 與
與![]() 軸有
軸有![]() 兩個焦點,且經過點
兩個焦點,且經過點![]()

(1)求![]() 的值;
的值;
(2)設![]()
![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的最小值;
的最小值;
(3)過![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與“羽毛球形線”相交于點
與“羽毛球形線”相交于點![]() 三點,問是否存在實數
三點,問是否存在實數![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從拋物線![]() 上任意一點P向x軸作垂線段,垂足為Q,點M是線段
上任意一點P向x軸作垂線段,垂足為Q,點M是線段![]() 上的一點,且滿足
上的一點,且滿足![]()
(1)求點M的軌跡C的方程;
(2)設直線![]() 與軌跡c交于
與軌跡c交于![]() 兩點,T為C上異于
兩點,T為C上異于![]() 的任意一點,直線
的任意一點,直線![]() ,
,![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點,以
兩點,以![]() 為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
為直徑的圓是否過x軸上的定點?若過定點,求出符合條件的定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.已知直線l上兩點M,N的極坐標分別為(2,0),(![]() ),圓C的參數方程
),圓C的參數方程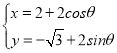 (θ為參數).
(θ為參數).
(Ⅰ)設P為線段MN的中點,求直線OP的平面直角坐標方程;
(Ⅱ)判斷直線l與圓C的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A4紙是生活中最常用的紙規格.A系列的紙張規格特色在于:①A0、A1、A2…、A5,所有尺寸的紙張長寬比都相同.②在A系列紙中,前一個序號的紙張以兩條長邊中點連線為折線對折裁剪分開后,可以得到兩張后面序號大小的紙,比如1張A0紙對裁后可以得到2張A1紙,1張A1紙對裁可以得到2張A2紙,依此類推.這是因為A系列紙張的長寬比為![]() :1這一特殊比例,所以具備這種特性.已知A0紙規格為84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1這一特殊比例,所以具備這種特性.已知A0紙規格為84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4紙的長度為( )
,那么A4紙的長度為( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓O及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉
旋轉![]() 而成,如圖2.已知圓O的半徑為
而成,如圖2.已知圓O的半徑為![]() ,設
,設![]() ,
,![]() ,圓錐的側面積為
,圓錐的側面積為![]() (S圓錐的側面積
(S圓錐的側面積![]() (R-底面圓半徑,I-母線長))
(R-底面圓半徑,I-母線長))
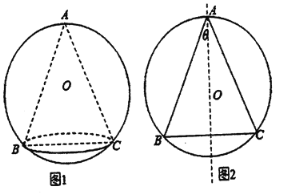
(1)求S關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積S最大.求S取得最大值時腰![]() 的長度
的長度
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com