【題目】高三學(xué)生為了迎接高考，要經(jīng)常進行模擬考試，鍛煉應(yīng)試能力，某學(xué)生從升入高三到高考要參加10次模擬考試，下面是高三第一學(xué)期某學(xué)生參加5次模擬考試的數(shù)學(xué)成績表：
模擬考試第x次 | 1 | 2 | 3 | 4 | 5 |
考試成績y分 | 90 | 100 | 105 | 105 | 100 |
（1）已知該考生的模擬考試成績y與模擬考試的次數(shù)x滿足回歸直線方程
，若高考看作第11次模擬考試，試估計該考生的高考數(shù)學(xué)成績；
（2）把這5次模擬考試的數(shù)學(xué)成績單放在5個相同的信封中，從中隨機抽取3份試卷的成績單進行研究，設(shè)抽取考試成績不等于平均值
的個數(shù)為
，求出的分布列與數(shù)學(xué)期望.
參考公式：
.
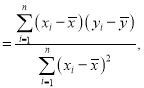
【答案】（1）120分, （2）分布列見解析，期望為
【解析】
（1）計算出
和
的值，然后將表格中的數(shù)據(jù)代入最小二乘法公式求出
和
的值，可求出回歸直線方程，然后將
代入回歸直線方程計算即可；
（2）由5次模擬考試的數(shù)學(xué)成績有
次與平均成績一致，即可得隨機變量
的所有可能取值為1，2，3，分別計算出概率，列出分布列求出數(shù)學(xué)期望.
（1）由表可知
，
，
，
，
則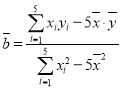
，
，
故回歸直線方程為
.
當時，
，
所以估計該考生的高考數(shù)學(xué)成績?yōu)?/span>120分.
（2）由題可知隨機變量的所有可能取值為1，2，3，
則
；
；
，
故隨機變量的分布列為：
| 1 | 2 | 3 |
P |
|
|
|
隨機變量的數(shù)學(xué)期望
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）求函數(shù)
在
上的單調(diào)遞增區(qū)間；
（2）將函數(shù)的圖象向左平移
個單位長度，再將圖象上所有點的橫坐標伸長到原來的
倍（縱坐標不變），得到函數(shù)
的圖象.求證：存在無窮多個互不相同的整數(shù)
，使得
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知點
，
分別是橢圓
的左頂點和上頂點，
為其右焦點，
，且該橢圓的離心率為
；
（1）求橢圓
的標準方程；
（2）設(shè)點
為橢圓上的一動點，且不與橢圓頂點重合，點
為直線
與
軸的交點，線段的中垂線與
軸交于點
，若直線
斜率為
，直線
的斜率為
，且
（
為坐標原點），求直線的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
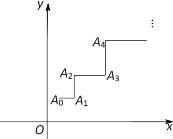
【題目】一青蛙從點
開始依次水平向右和豎直向上跳動，其落點坐標依次是
，(如圖，的坐標以已知條件為準)，
表示青蛙從點
到點
所經(jīng)過的路程.
(1)點為拋物線
準線上一點，點
，
均在該拋物線上，并且直線經(jīng)過該拋物線的焦點，證明
；
(2)若點
要么落在
所表示的曲線上，要么落在
所表示的曲線上，并且
,試寫出
(不需證明)；
(3)若點
要么落在
所表示的曲線上，要么落在
所表示的曲線上，并且
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知離心率為
的橢圓
的左頂點為A，且橢圓E經(jīng)過
與坐標軸不垂直的直線l與橢圓E交于C，D兩點，且直線AC和直線AD的斜率之積為
.
（I）求橢圓E的標準方程；
（Ⅱ）求證：直線l過定點.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，下列說法正確的是__________.
的值域是
；
當
時，方程
有兩個不等實根；
若函數(shù)
有三個零點時，則
；
經(jīng)過
有三條直線與
相切.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】日照一中為了落實“陽光運動一小時”活動，計劃在一塊直角三角形ABC的空地上修建一個占地面積為S的矩形AMPN健身場地．如圖，點M在AC上，點N在AB上，且P點在斜邊BC上，已知∠ACB=60°且|AC|=30米，|AM|=x米，x∈[10，20]．
（1）試用x表示S，并求S的取值范圍；
（2）若在矩形AMPN以外（陰影部分）鋪上草坪．已知：矩形AMPN健身場地每平方米的造價為
，草坪的每平方米的造價為
（k為正常數(shù)）．設(shè)總造價T關(guān)于S的函數(shù)為T=f（S），試問：如何選取|AM|的長，才能使總造價T最低．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】（文科）已知四棱錐
的底面ABCD為直角梯形，
，
，
，
為正三角形.
（1）點M為棱AB上一點，若
平面SDM，
，求實數(shù)λ的值；
（2）若
，求四棱錐的體積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
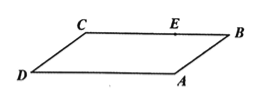
【題目】如圖，有一塊平行四邊形綠地
，經(jīng)測量
百米，
百米，
，擬過線段
上一點
設(shè)計一條直路
（點
在四邊形
的邊上，不計路的寬度），
將綠地分成兩部分，且右邊面積是左邊面積的3倍，設(shè)
百米，
百米．
（1）當點
與點
重合時，試確定點
的位置；
（2）試求
的值，使路
的長度
最短．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
