
 如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E是棱BC的中點,點F在棱CC1上,且CF=2FC1,P是側面四邊形BCC1B1內一點(含邊界),若A1P∥平面AEF,則直線A1P與面BCC1B1所成角的正弦值的取值范圍是( )
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E是棱BC的中點,點F在棱CC1上,且CF=2FC1,P是側面四邊形BCC1B1內一點(含邊界),若A1P∥平面AEF,則直線A1P與面BCC1B1所成角的正弦值的取值范圍是( )| A. | $[\frac{{2\sqrt{5}}}{5},\frac{{5\sqrt{29}}}{29}]$ | B. | $[\frac{{3\sqrt{13}}}{13},\frac{{5\sqrt{29}}}{29}]$ | C. | $[\frac{{3\sqrt{13}}}{13},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{2\sqrt{5}}}{5},\frac{{2\sqrt{2}}}{3}]$ |
分析 分別取棱BB1、B1C1的中點M、N,連接MN,易證平面A1MN∥平面AEF,由題意知點P必在線段MN上,由此可判斷P在M或N處時A1P最長,位于線段MN中點處時最短,通過解直角三角形即可求得.
解答 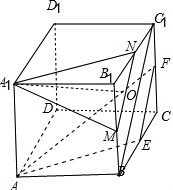 解:如下圖所示:
解:如下圖所示:
分別取棱BB1、B1C1的中點M、N,連接MN,連接BC1,
∵M、N、E、F為所在棱的中點,∴MN∥BC1,EF∥BC1,
∴MN∥EF,又MN?平面AEF,EF?平面AEF,
∴MN∥平面AEF;
∵AA1∥NE,AA1=NE,∴四邊形AENA1為平行四邊形,
∴A1N∥AE,又A1N?平面AEF,AE?平面AEF,
∴A1N∥平面AEF,
又A1N∩MN=N,∴平面A1MN∥平面AEF,
∵P是側面BCC1B1內一點,且A1P∥平面AEF,
則P必在線段MN上,
在Rt△A1B1M中,A1M=$\sqrt{{A}_{1}{{B}_{1}}^{2}+{B}_{1}{M}^{2}}$=$\sqrt{1+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
同理,在Rt△A1B1N中,求得A1N=$\frac{\sqrt{5}}{2}$,
∴△A1MN為等腰三角形,
當P在MN中點O時A1P⊥MN,此時A1P最短,P位于M、N處時A1P最長,
A1O=$\sqrt{{A}_{1}{M}^{2}-O{M}^{2}}$=$\sqrt{(\frac{\sqrt{5}}{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}$=$\frac{3\sqrt{2}}{4}$,
A1M=A1N=$\frac{\sqrt{5}}{2}$,
所以線段A1P長度的取值范圍是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
直線A1P與面BCC1B1所成角的正弦值的最小值為:$\frac{1}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$.
直線A1P與面BCC1B1所成角的正弦值最大值為:$\frac{1}{\frac{3\sqrt{2}}{4}}$=$\frac{2\sqrt{2}}{3}$.
直線A1P與面BCC1B1所成角的正弦值的取值范圍是:[$\frac{2\sqrt{5}}{5}$,$\frac{2\sqrt{2}}{3}$].
故選:D.
點評 本題考查點、線、面間的距離問題,考查學生的運算能力及推理轉化能力,屬中檔題,解決本題的關鍵是通過構造平行平面尋找P點位置.


科目:高中數學 來源: 題型:選擇題
| A. | ${log_{\frac{1}{3}}}5$ | B. | 5 | C. | -5 | D. | ${({\frac{1}{3}})^5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $16\sqrt{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{3}$ | B. | -$\frac{7}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{9}{4}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com