
已知各項為正數的數列 滿足
滿足 (
( ),且
),且 是
是 的等差中項,則數列
的等差中項,則數列 的通項公式是 .
的通項公式是 .
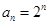
【解析】
試題分析:∵an+12-an+1an-2an2=0,∴(an+1+an)(an+1-2an)=0,∵數列{an}的各項均為正數,∴an+1+an>0,∴an+1-2an=0,即an+1=2an,所以數列{an}是以2為公比的等比數列.∵a3+2是a2,a4的等差中項,∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,∴a1=2,∴數列{an}的通項公式an=2n.
考點:本題考查了數量的遞推關系
點評:數列是高中數學的重要內容,又是學習高等數學的基礎,所以在高考中占有重要的地位.高考對本章的考查比較全面,等差數列,等比數列的考查每年都不會遺漏,屬于中檔題


科目:高中數學 來源: 題型:
| bn | an |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源:2012屆浙江省學軍中學高三上學期理科數學期中考試試卷 題型:解答題
已知各項為正數的數列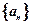 的前
的前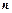 項和為
項和為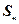 ,且滿足
,且滿足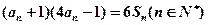 ,
,
(1)求數列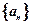 的通項公式
的通項公式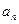
(2)令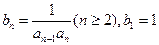 ,數列
,數列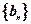 的前
的前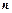 項和為
項和為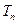 ,若
,若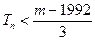 對一切
對一切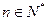 恒成立,求
恒成立,求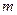 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省高三上學期理科數學期中考試試卷 題型:解答題
已知各項為正數的數列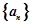 的前
的前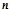 項和為
項和為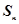 ,且滿足
,且滿足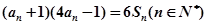 ,
,
(1)求數列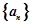 的通項公式
的通項公式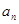
(2)令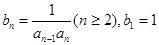 ,數列
,數列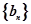 的前
的前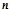 項和為
項和為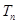 ,若
,若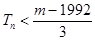 對一切
對一切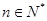 恒成立,求
恒成立,求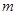 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com