
分析 對f(x)求導(dǎo),討論f′(x)的正負(fù)以及對應(yīng)f(x)的單調(diào)性,得出函數(shù)y=f(x)有兩個零點的等價條件,從而求出a的取值范圍;
解答 解:∵f(x)=aex-x,∴f′(x)=aex-1;
下面分兩種情況討論:
①a≤0時,f′(x)<0在R上恒成立,∴f(x)在R上是減函數(shù),不合題意;
②a>0時,由f′(x)=0,得x=-lna,當(dāng)x變化時,f′(x)、f(x)的變化情況如下表:
| x | (-∞,-lna) | -lna | (-lna,+∞) |
| f′(x) | - | 0 | +- |
| f(x) | 遞減 | 極小值-lna-1 | 遞增 |
點評 本題考查了導(dǎo)數(shù)的運算以及利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性與零點問題,也考查了函數(shù)思想、化歸思想和分析問題、解決問題的能力.


科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
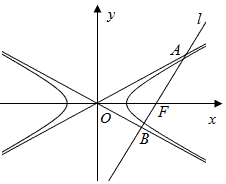 如圖所示,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,過F的直線l交雙曲線的漸近線于A,B兩點,且直線l的傾斜角是漸近線OA傾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,則該雙曲線的離心率為$\frac{2\sqrt{3}}{3}$.
如圖所示,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點為F,過F的直線l交雙曲線的漸近線于A,B兩點,且直線l的傾斜角是漸近線OA傾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,則該雙曲線的離心率為$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{24}{25}$ | B. | -$\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{19}$ | D. | 19 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com