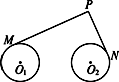
如圖，圓O1與圓O2的半徑都是1，O1O2＝4，過動點P分別作圓O1、圓O2的切線PM、PN(M、N分別為切點)，使得PM＝
PN，試建立適當的坐標系，并求動點P的軌跡方程．
|
解：如圖，以直線O1O2為x軸，線段O1O2的垂直平分線為y軸，建立平面直角坐標系，則兩圓心分別為O1(－2，0)，O2(2，0)．
設P(x，y)，則PM2＝O1P2－O1M2＝(x＋2)2＋y2－1．同理，PN2＝(x－2)2＋y2－1． ∵PM＝ ∴(x＋2)2＋y2－1＝2［(x－2)2＋y2－1］，即x2－12x＋y2＋3＝0， 即 
練習冊系列答案
相關習題
科目：高中數學 來源： 題型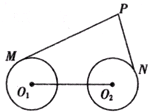：  如圖，圓O1與圓O2的半徑都是1，O1O2=4，過動點P分別作圓O1．圓O2的切線PM、PN（M．N分別為切點），使得PM=
查看答案和解析>> 科目：高中數學 來源： 題型：  A．選修4-1：幾何證明選講如圖，圓O1與圓O2內切于點A，其半徑分別為r1與r2（r1＞r2 ）．圓O1的弦AB交圓O2于點C （ O1不在AB上）．求證：AB：AC為定值． B．選修4-2：矩陣與變換 已知矩陣A=
C．選修4-4：坐標系與參數方程 在平面直角坐標系xOy中，求過橢圓
D．選修4-5：不等式選講（本小題滿分10分） 解不等式：x+|2x-1|＜3． 查看答案和解析>> 科目：高中數學 來源：2011-2012學年河北省高三第一次模擬考試理科數學試卷（解析版） 題型：解答題 如圖，圓O1與圓O2相交于A、B兩點，AB是圓O2的直徑，過A點作圓O1的切線交圓O2于點E，并與BO1的延長線交于點P，PB分別與圓O1、圓O2交于C，D兩點. 求證：(Ⅰ)PA·PD=PE·PC； (Ⅱ)AD=AE.
查看答案和解析>> 同步練習冊答案 湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區 違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com版權聲明：本站所有文章，圖片來源于網絡，著作權及版權歸原作者所有，轉載無意侵犯版權，如有侵權，請作者速來函告知，我們將盡快處理，聯系qq：3310059649。 ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號 |
PN，
圓O1與圓O2相交于A、B，過A作圓O1的切線交圓O2于C，連CB并延長交圓O1于D，連AD，AB=2，BD=3，BC=5，求AD的長．