
已知函數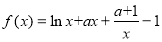 .
.
(1)當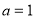 時,求曲線
時,求曲線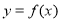 在點
在點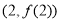 處的切線方程;
處的切線方程;
(2)當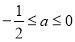 時,討論
時,討論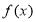 的單調性.
的單調性.
(1)
(2)當 時,在
時,在 ,
, 單調遞減,在
單調遞減,在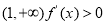 ,
, 單調遞增;
單調遞增;
當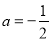 時,在
時,在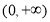 單調遞減
單調遞減
當 時,在
時,在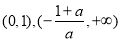
 單調遞減,
單調遞減, 在
在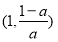 單調遞增;
單調遞增;
【解析】
試題分析:(1)利用切點處的導函數值是切線的斜率,應用直線方程的點斜式即得;
(2)求導數 ,
,
根據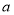 的不同取值情況,研究導數值的正負,確定函數的單調性.
的不同取值情況,研究導數值的正負,確定函數的單調性.
本題易錯,分類討論不全或重復.
試題解析:(1)當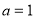 時,
時,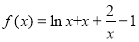 ,
,
此時 , 2分
, 2分
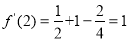 ,又
,又 ,
,
所以切線方程為: ,
,
整理得: ;
;  分
分
(2) , 6分
, 6分
當 時,
時, ,此時,在
,此時,在 ,
, 單調遞減,
單調遞減,
在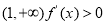 ,
, 單調遞增; 8分
單調遞增; 8分
當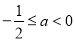 時,
時, ,
,
當 即
即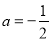 時
時 在
在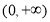 恒成立,
恒成立,
所以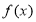 在
在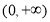 單調遞減; 10分
單調遞減; 10分
當 時,
時, ,此時在
,此時在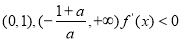 ,
, 單調遞減,
單調遞減, 在
在 單調遞增; 12分
單調遞增; 12分
綜上所述:當 時,
時, 在
在 單調遞減,
單調遞減, 在
在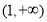 單調遞增;
單調遞增;
當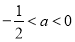 時,
時,  在
在 單調遞減,
單調遞減, 在
在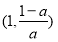 單調遞增;
單調遞增;
當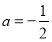 時
時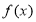 在
在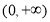 單調遞減. 13分
單調遞減. 13分
考點:應用導數研究函數的單調性,導數的幾何意義,直線方程的點斜式.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源:2015屆吉林省吉林市高三第一次摸底考試理科數學試卷(解析版) 題型:選擇題
將函數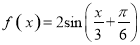 的圖象向左平移
的圖象向左平移 個單位,再向下平移1個單位,得到函數 g( x)的圖象,則 g( x)的解析式為( )
個單位,再向下平移1個單位,得到函數 g( x)的圖象,則 g( x)的解析式為( )
A. B.
B.
C.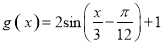 D.
D.
查看答案和解析>>
科目:高中數學 來源:2015屆北京市朝陽區高三上學期期中統一考試理科數學試卷(解析版) 題型:選擇題
設函數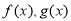 滿足下列條件:
滿足下列條件:
(1)對任意實數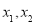 都有
都有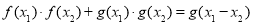 ;
;
(2)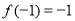 ,
,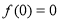 ,
,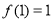 .
.
下列四個命題:
①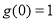 ;
;
② ;
;
③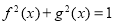 ;
;
④當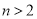 ,
,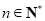 時,
時,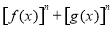 的最大值為
的最大值為 .
.
其中所有正確命題的序號是( )
A.①③ B.②④ C.②③④ D.①③④
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省煙臺市高三統一質量檢測考試文科數學試卷(解析版) 題型:解答題
已知數列 的前
的前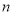 項和為
項和為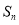 ,且
,且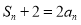 ,數列
,數列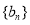 滿足
滿足 ,且
,且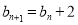 .
.
(1)求數列 ,
,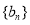 的通項公式;
的通項公式;
(2)設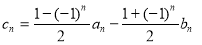 ,求數列
,求數列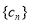 的前
的前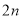 項和
項和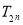 .
.
查看答案和解析>>
科目:高中數學 來源:2015屆北京市朝陽區高三上學期期中統一考試文科數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知數列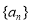 是等差數列,且
是等差數列,且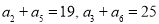 .
.
(Ⅰ)求數列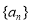 的通項公式;
的通項公式;
(Ⅱ)若數列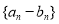 是首項為2,公比為2的等比數列,求數列
是首項為2,公比為2的等比數列,求數列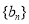 的前
的前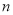 項和
項和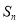 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省煙臺市高三統一質量檢測考試文科數學試卷(解析版) 題型:填空題
已知拋物線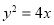 的準線與雙曲線
的準線與雙曲線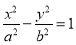 的兩條漸近線分別交于
的兩條漸近線分別交于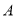 ,
,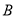 兩點,且
兩點,且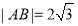 ,則雙曲線的離心率
,則雙曲線的離心率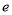 為 .
為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省煙臺市高三5月適應性訓練一文科數學試卷(解析版) 題型:解答題
某數學興趣小組有男女生各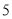 名.以下莖葉圖記錄了該小組同學在一次數學測試中的成績(單位:分).已知男生數據的中位數為
名.以下莖葉圖記錄了該小組同學在一次數學測試中的成績(單位:分).已知男生數據的中位數為 ,女生數據的平均數為
,女生數據的平均數為 .
.
(1)求 ,
, 的值;
的值;
(2)現從成績高于 分的同學中隨機抽取兩名同學,求抽取的兩名同學恰好為一男一女的概率.
分的同學中隨機抽取兩名同學,求抽取的兩名同學恰好為一男一女的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com