
【題目】已知下面四個命題:
①“若![]() ,則
,則![]() 或
或![]() ”的逆否命題為“若
”的逆否命題為“若![]() 且
且![]() ,則
,則![]() ”
”
②命題:“![]() ,若
,若![]() ,則
,則![]() ”,用反證法證明時應假設
”,用反證法證明時應假設![]() 或
或![]() .
.
③命題![]() 存在
存在![]() ,使得
,使得![]() ,則
,則![]() :任意
:任意![]() ,都有
,都有![]()
④若![]() 且
且![]() 為假命題,則
為假命題,則![]() 均為假命題,其中真命題個數為( )
均為假命題,其中真命題個數為( )
A.1B.2C.3D.4
科目:高中數學 來源: 題型:
【題目】直角坐標系![]() 中,圓
中,圓![]()
![]() (
(![]() 為參數)上的每一點的橫坐標不變,縱坐標變為原來的
為參數)上的每一點的橫坐標不變,縱坐標變為原來的![]() ,得到曲線
,得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 與兩坐標軸分別相交于
與兩坐標軸分別相交于![]() 兩點,點
兩點,點![]() 在
在![]() 上,求
上,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=4x的焦點為F,準線為l,過l上一點P作拋物線C的兩條切線,切點為A,B.
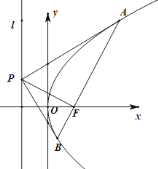
(1)求證:直線AB過焦點F;
(2)若|PA|=8,|PB|=6,求|PF|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,若△
,若△![]() 的三個頂點都在拋物線
的三個頂點都在拋物線![]() 上,且
上,且![]() ,則稱該三角形為“核心三角形”.
,則稱該三角形為“核心三角形”.
(1)是否存在“核心三角形”,其中兩個頂點的坐標分別為![]() 和
和![]() ?請說明理由;
?請說明理由;
(2)設“核心三角形”![]() 的一邊
的一邊![]() 所在直線的斜率為4,求直線
所在直線的斜率為4,求直線![]() 的方程;
的方程;
(3)已知△![]() 是“核心三角形”,證明:點
是“核心三角形”,證明:點![]() 的橫坐標小于2.
的橫坐標小于2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]()
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)若![]() ,是否存在q的某些取值,使數列
,是否存在q的某些取值,使數列![]() 中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使數列
,使數列![]() 中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】CPI是居民消費價格指數(comsummer priceindex)的簡稱.居民消費價格指數是一個反映居民家庭一般所購買的消費品價格水平變動情況的宏觀經濟指標.如圖是根據國家統計局發布的2019年4月——2020年4月我國CPI漲跌幅數據繪制的折線圖(注:2019年6月與2018年6月相比較,叫同比;2019年6月與2019年5月相比較,叫環比),根據該折線圖,則下列結論正確的是( )
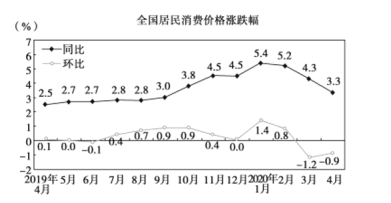
A.2019年4月至2020年4月各月與去年同期比較,CPI有漲有跌
B.2019年4月居民消費價格同比漲幅最小,2020年1月同比漲幅最大
C.2020年1月至2020年4月CPI只跌不漲
D.2019年4月至2019年6月CPI漲跌波動不大,變化比較平穩
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com