
(本小題12分)等差數列 的前
的前 項和記為
項和記為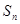 ,已知
,已知 .
.
(1)求數列 的通項
的通項 ;(2)若
;(2)若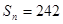 ,求
,求 ;(3)令
;(3)令 ,求數列
,求數列 的前
的前 項和
項和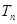 .
.
(1)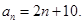 ;(2)
;(2)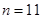 ;(3)
;(3)

解析試題分析:(1)由 可建立關于a1和d的方程,解出a1和d的值,得到數列
可建立關于a1和d的方程,解出a1和d的值,得到數列 的通項
的通項 .(2)根據
.(2)根據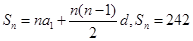 可建立關于n的方程解出n的值.
可建立關于n的方程解出n的值.
(3)因為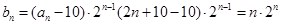 ,顯然應采用錯位相減的方法求和.
,顯然應采用錯位相減的方法求和.
(1)由 ,得方程組
,得方程組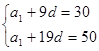 ,
,
解得
 .....................3分
.....................3分
(2)由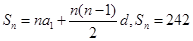 得方程
得方程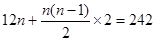
解得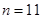 或
或 (舍去),
(舍去),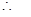
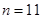 .....................6分
.....................6分
(3)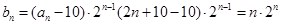 .....................7分
.....................7分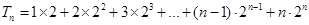
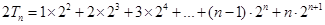 .....................9分
.....................9分
兩式相減得: .....................10分
.....................10分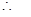

=-
 =
= .....................12分
.....................12分
考點:等差數列的通項公式及前n項和公式,以及錯位相減法求和.
點評:錯位相減法求和主要適應用一個等差數列與一個等比數列對應項的積構成的數列,其前n項和可考慮錯位相減法.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知函數 的圖像經過點
的圖像經過點 .
.
(1)求該函數的解析式;
(2)數列 中,若
中,若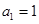 ,
, 為數列
為數列 的前
的前 項和,且滿足
項和,且滿足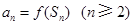 ,
,
證明數列 成等差數列,并求數列
成等差數列,并求數列 的通項公式;
的通項公式;
(3)另有一新數列 ,若將數列
,若將數列 中的所有項按每一行比上一行多一項的規則排成
中的所有項按每一行比上一行多一項的規則排成
如下數表:
 |
  |
   |
    |
 構成的數列即為數列
構成的數列即為數列 ,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當
,上表中,若從第三行起,第一行中的數按從左到右的順序均構成等比數列,且公比為同一個正數.當 時,求上表中第
時,求上表中第 行所有項的和.
行所有項的和.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com