日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

(1)求數列1，，，…，的通項公式an

(2)求數列{an}的前n項和

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

在數列{an}中，a1=1，a2=
2
，Sn是數列{an}的前n項和．當n≥2且n∈N*時，Sn+1(Sn+1-2Sn)+(2Sn-Sn-1)Sn-1=1，令bn=
a
4
n
(
1
a
4
1
+
1
a
4
2
+
1
a
4
3
+…+
1
a
4
n-1
)．
（1）求數列{an}的通項公式；試用n和bn表示bn+1；
（2）若b1=1，n∈N*，證明：(1+
1
b1
)(1+
1
b2
)…(1+
1
bn
)＞
29
9
-
2(n+1)
n(n+2)
．
（3）當n∈N*時，證明
a
2
1
C
0
n
2
+
a
2
2
C
1
n
22
+
a
2
3
C
2
n
23
+…+
a
2
i+1
C
1
n
2i+1
+…+
a
2
n+1
C
n
n
2n+1
≤3n-1．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知數列{an}滿足:a1=2,an+1=2(1+)2an.

(1)求數列{an}的通項公式;

(2)設bn=(An2+Bn+C)·2n,試推斷是否存在常數A，B，C，使對一切n∈N*都有an=bn+1-bn成立？說明你的理由;

(3)求證：a1+a2+a3+…+an≥2n+2-6.

查看答案和解析>>

科目：高中數學 來源：2014屆江蘇省南通市高一下學期期中數學試卷（解析版） 題型：解答題

 已知數列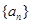的前n項和為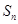,且,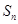

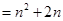(1)求數列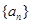的通項公式;

(2) 令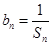，且數列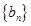的前n項和為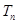，求;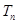

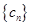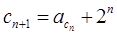(3)若數列滿足條件：，又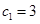，是否存在實數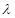，使得數列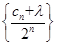為等差數列?

 

查看答案和解析>>

科目：高中數學 來源： 題型：

設f(x)=(0＜x＜1),

(1)求f-1(x);

(2)設a1=1,an+1=f-1(an),求數列{an}的通項公式;

(3)在(2)的條件下,又設b1=,bn+1=(1+bn)2f-1(bn),

證明n≥2時,有1＜++…+＜2.

查看答案和解析>>

科目：高中數學 來源： 題型：

在直角坐標平面上有一點列Pn(xn,yn)(n∈N*),點Pn位于直線y=3x+上,且Pn的橫坐標構成以為首項,-1為公差的等差數列{xn}.

(1)求點Pn的坐標;

(2)設拋物線列C1,C2,…,Cn,…中的每一條的對稱軸都垂直于x軸,第n條拋物線Cn的頂點為Pn,且經過點Dn(0,n2+1)(n∈N*).記與拋物線Cn相切于點Dn的直線的斜率為kn,求證:++…+＜;

(3)設S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差數列{an}的任意一項an∈S∩T,其中a1是S∩T中的最大數,且-256＜a10＜-125,求數列{an}的通項公式.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 依人99| 亚洲一区二区三区高清 | 日韩欧美区 | 久久99精品视频 | 精品亚洲一区二区三区 | 亚洲欧美日本在线 | 亚洲国产精品久久 | 激情综合色 | 黄色影音 | 免费观看黄a一级视频 | 9999国产精品欧美久久久久久 | 欧美一区免费 | 老司机福利在线视频 | 久久精品欧美一区二区三区不卡 | 日韩一区二区高清 | 日本在线观看不卡 | 国产精品美女www爽爽爽软件 | 毛片99 | 国产精品18 | 国产一区在线视频 | 久久精品视频99 | 国产香蕉网 | 日本免费一区二区视频 | 亚洲激情一区 | 国产成人久久精品一区二区三区 | 国产乱码精品一区二区 | 久久精品国产一区二区三区不卡 | 欧美视频网站 | 久久久一区二区三区捆绑sm调教 | 日本三级网站在线观看 | 日韩一区二区在线视频 | 一区二区日韩精品 | 国产日本欧美一区二区三区 | 国产一区二区精品 | 一区二区免费 | 欧美精三区欧美精三区 | 欧美成人在线网站 | 久草青青| 色丁香婷婷 | 国产成人精品一区二区三区 | 国产精品久久久久久久久久久久久 |