
【題目】如圖,已知![]() 與
與![]() 分別是邊長為1與2的正三角形,
分別是邊長為1與2的正三角形,![]() ,四邊形
,四邊形![]() 為直角梯形,且
為直角梯形,且![]() ,
,![]() ,點
,點![]() 為
為![]() 的重心,
的重心,![]() 為
為![]() 中點,
中點,![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的三等分點.
的三等分點.
(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,試求異面直線
,試求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
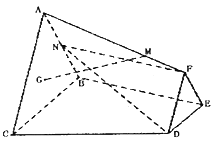
【答案】(1)見解析(2)![]()
【解析】分析:(1)連![]() 并延長交
并延長交![]() 于
于![]() ,連
,連![]() ,由三角形的重心的條件及題意可得
,由三角形的重心的條件及題意可得![]() ,故
,故![]() ,再根據線面平行的判定定理可得結論.(2)由題意得
,再根據線面平行的判定定理可得結論.(2)由題意得![]() 兩兩垂直,由此建立空間直角坐標系.設
兩兩垂直,由此建立空間直角坐標系.設![]() ,結合條件求得平面
,結合條件求得平面![]() 的法向量為
的法向量為![]() ,又平面
,又平面![]() 的法向量為
的法向量為![]() ,根據二面角的余弦值為
,根據二面角的余弦值為![]() 可求得
可求得![]() ,進而可求得異面直線
,進而可求得異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
詳解:(1)證明:在![]() 中,連
中,連![]() 并延長交
并延長交![]() 于
于![]() ,連
,連![]() .
.

因為點![]() 為
為![]() 的重心,
的重心,
所以![]() ,且
,且![]() 為
為![]() 中點.
中點.
又![]() ,
,
所以![]() ,
,
所以![]() .
.
又![]() 為
為![]() 中點,
中點,
所以![]() .
.
又![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() 四點共面,
四點共面,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由題意,![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
因為平面![]() 平面
平面![]() ,且交線為
,且交線為![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 與
與![]() 分別是邊長為1與2的正三角形,
分別是邊長為1與2的正三角形,
故以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸建立如圖所示的空間直角坐標系
軸建立如圖所示的空間直角坐標系![]() .
.

設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因為![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
由 ,得
,得 ,
,
令![]() ,得
,得![]() .
.
又平面![]() 的法向量
的法向量![]() .
.
由題意得![]() ,
,
解得![]() ,
,
又![]() ,
,![]() ,
,
所以![]()

![]() .
.
所以異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】為建設美麗鄉村,政府欲將一塊長12百米,寬5百米的矩形空地ABCD建成生態休閑園,園區內有一景觀湖EFG(圖中陰影部分).以AB所在直線為x軸,AB的垂直平分線為y軸,建立平面直角坐標系xOy(如圖所示).景觀湖的邊界曲線符合函數![]() 模型.園區服務中心P在x軸正半軸上,PO=
模型.園區服務中心P在x軸正半軸上,PO=![]() 百米.
百米.

(1)若在點O和景觀湖邊界曲線上一點M之間修建一條休閑長廊OM,求OM的最短長度;
(2)若在線段DE上設置一園區出口Q,試確定Q的位置,使通道直線段PQ最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是由
是由![]() 個有序實數構成的一個數組,記作:
個有序實數構成的一個數組,記作:![]() .其中
.其中![]() 稱為數組
稱為數組![]() 的“元”,
的“元”,![]() 為
為![]() 的下標.如果數組
的下標.如果數組![]() 中的每個“元”都來自數組
中的每個“元”都來自數組![]() 中不同下標的“元”則稱
中不同下標的“元”則稱![]() 為
為![]() 的子數組.定義兩個數組
的子數組.定義兩個數組![]() ,
,![]() 的關系數為
的關系數為![]() .
.
(1)若![]() ,
,![]() ,設
,設![]() 是
是![]() 的含有兩個“元”的子數組,求
的含有兩個“元”的子數組,求![]() 的最大值及此時的數組
的最大值及此時的數組![]() ;
;
(2)若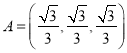 ,
,![]() ,且
,且![]() ,
,![]() 為
為![]() 的含有三個“元”的子數組,求
的含有三個“元”的子數組,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵、網購、移動支付和共享單車被譽為中國的“新四大發明”,彰顯出中國式創新的強勁活力.某移動支付公司從我市移動支付用戶中隨機抽取100名進行調查,得到如下數據:
每周移動支付次數 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合計 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移動支付6次及6次以上的用戶稱為“移動支付達人”,按分層抽樣的方法,在我市所有“移動支付達人”中,隨機抽取6名用戶
求抽取的6名用戶中,男女用戶各多少人;
② 從這6名用戶中抽取2人,求既有男“移動支付達人”又有女“移動支付達人”的概率.
(2)把每周使用移動支付超過3次的用戶稱為“移動支付活躍用戶”,填寫下表,問能否在犯錯誤概率不超過0.01的前提下,認為“移動支付活躍用戶”與性別有關?
P(χ2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | .635 |

非移動支付活躍用戶 | 移動支付活躍用戶 | 合計 | |
男 | |||
女 | |||
合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有120粒試驗種子需要播種,現有兩種方案:方案一:將120粒種子分種在40個坑內,每坑3粒;方案二:120粒種子分種在60個坑內,每坑2粒 如果每粒種子發芽的概率為0.5,并且,若一個坑內至少有1粒種子發芽,則這個坑不需要補種;若一個坑內的種子都沒發芽,則這個坑需要補種(每個坑至多補種一次,且第二次補種的種子顆粒同第一次).假定每個坑第一次播種需要2元,補種1個坑需1元;每個成活的坑可收貨100粒試驗種子,每粒試驗種子收益1元.
(1)用![]() 表示播種費用,分別求出兩種方案的
表示播種費用,分別求出兩種方案的![]() 的數學期望;
的數學期望;
(2)用![]() 表示收益,分別求出兩種方案的收益
表示收益,分別求出兩種方案的收益![]() 的數學期望;
的數學期望;
(3)如果在某塊試驗田對該種子進行試驗,你認為應該選擇哪種方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 與圓
與圓![]() 外切于原點
外切于原點![]() ,且兩圓圓心的距離
,且兩圓圓心的距離![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求圓![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)過點![]() 的直線
的直線![]() 、
、![]() 與圓
與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() 和點
和點![]() ,與圓
,與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() 和點
和點![]() ,且
,且![]() .求四邊形
.求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古代“五行”學認為:“物質分金、木、土、水、火五種屬性,金克木,木克土,土克水,水克火,火克金.”將五種不同屬性的物質任意排成一列,但排列中屬性相克的兩種物質不相鄰,則這樣的排列方法有
A.5種B.10種
C.20種D.120種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com