
【題目】設函數![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)設![]() .對任意
.對任意![]() ,都有
,都有![]() ,
,
求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]()
【解析】
試題分析:(1)由題已知![]() ,可得函數
,可得函數![]() 解析式,求函數的單調區間和極值。可先求函數的導數,令
解析式,求函數的單調區間和極值。可先求函數的導數,令![]() ,為增區間,反之為減區間,再判斷出極值。
,為增區間,反之為減區間,再判斷出極值。
(2)由條件![]() 變形(聯想函數的單調性),然后構造函數
變形(聯想函數的單調性),然后構造函數![]() ,問題轉化為求
,問題轉化為求![]() 在
在![]() 上單調遞減,得分段函數,需分情況討論,可得
上單調遞減,得分段函數,需分情況討論,可得![]() 的取值范圍。
的取值范圍。
分別根據單調性和極值情況解出![]() 的值,最后取它們的并集得出。
的值,最后取它們的并集得出。
試題解析:(1)當![]() 時,
時,![]() ,定義域為
,定義域為![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
綜上,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ,
,
所以.![]()
(2)由題意得![]() ,即
,即![]() ,
,
若設![]() ,則
,則![]() 在
在![]() 上單調遞減,
上單調遞減,
又
①當![]() 時,
時,![]() ,
,![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
設![]() ,則
,則![]() ,當
,當![]() 時,
時,![]() ,
,
![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,∴
,∴![]() .
.
②當![]() 時,
時,![]() ,
,![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
設![]() ,則
,則![]() ,
,
即![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,∴
,∴![]() . 綜上,由①②可得
. 綜上,由①②可得![]() .
.


 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:高中數學 來源: 題型:
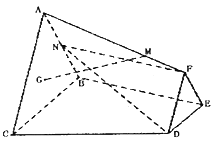
【題目】如圖,已知![]() 與
與![]() 分別是邊長為1與2的正三角形,
分別是邊長為1與2的正三角形,![]() ,四邊形
,四邊形![]() 為直角梯形,且
為直角梯形,且![]() ,
,![]() ,點
,點![]() 為
為![]() 的重心,
的重心,![]() 為
為![]() 中點,
中點,![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的三等分點.
的三等分點.
(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,試求異面直線
,試求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】東莞市攝影協會準備在2019年10月舉辦主題為“慶祖國70華誕——我們都是追夢人”攝影圖片展.通過平常人的鏡頭記錄國強民富的幸福生活,向祖國母親的生日獻禮,攝影協會收到了來自社會各界的大量作品,打算從眾多照片中選取100張照片展出,其參賽者年齡集中在![]() 之間,根據統計結果,做出頻率分布直方圖如圖:
之間,根據統計結果,做出頻率分布直方圖如圖:

(1)求頻率分布直方圖中![]() 的值,并根據頻率分布直方圖,求這100位攝影者年齡的樣本平均數
的值,并根據頻率分布直方圖,求這100位攝影者年齡的樣本平均數![]() 和中位數
和中位數![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(2)為了展示不同年齡作者眼中的祖國形象,攝影協會按照分層抽樣的方法,計劃從這100件照片中抽出20個最佳作品,并邀請相應作者參加“講述照片背后的故事”座談會.
①在答題卡上的統計表中填出每組相應抽取的人數:
年齡 |
|
|
|
|
|
人數 |
②若從年齡在![]() 的作者中選出2人把這些圖片和故事整理成冊,求這2人至少有一人的年齡在
的作者中選出2人把這些圖片和故事整理成冊,求這2人至少有一人的年齡在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了參加某數學競賽,某高級中學對高二年級理科、文科兩個數學興趣小組的同學進行了賽前模擬測試,成績(單位:分)記錄如下.
理科:79,81,81,79,94,92,85,89
文科:94,80,90,81,73,84,90,80
畫出理科、文科兩組同學成績的莖葉圖;

(2)計算理科、文科兩組同學成績的平均數和方差,并從統計學的角度分析,哪組同學在此次模擬測試中發揮比較好;
(3)若在成績不低于90分的同學中隨機抽出3人進行培訓,求抽出的3人中既有理科組同學又有文科組同學的概率.
(參考公式:樣本數據x1,x2,…,xn的方差:
s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2+…+(xn-
)2+…+(xn-![]() )2],其中
)2],其中![]() 為樣本平均數)
為樣本平均數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校開展一次“五![]() 四”知識競賽活動,共有三個問題,其中第1、2題滿分都是15分,第3題滿分是20分.每個問題或者得滿分,或者得0分.活動結果顯示,每個參賽選手至少答對一道題,有6名選手只答對其中一道題,有12名選手只答對其中兩道題.答對第1題的人數與答對第2題的人數之和為26,答對第1的人數與答對第3題的人數之和為24,答對第2題的人數與答對第3題的人數之和為22.則參賽選手中三道題全答對的人數是____;所有參賽選手的平均分是____.
四”知識競賽活動,共有三個問題,其中第1、2題滿分都是15分,第3題滿分是20分.每個問題或者得滿分,或者得0分.活動結果顯示,每個參賽選手至少答對一道題,有6名選手只答對其中一道題,有12名選手只答對其中兩道題.答對第1題的人數與答對第2題的人數之和為26,答對第1的人數與答對第3題的人數之和為24,答對第2題的人數與答對第3題的人數之和為22.則參賽選手中三道題全答對的人數是____;所有參賽選手的平均分是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且兩焦點與短軸的一個頂點的連線構成等腰直角三角形.
,且兩焦點與短軸的一個頂點的連線構成等腰直角三角形.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點,試問:是否存在一個定點
兩點,試問:是否存在一個定點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假定生男孩和生女孩是等可能的,令![]() {一個家庭中既有男孩又有女孩},
{一個家庭中既有男孩又有女孩},![]() {一個家庭中最多有一個女孩}.對下述兩種情形,討論
{一個家庭中最多有一個女孩}.對下述兩種情形,討論![]() 與
與![]() 的獨立性.
的獨立性.
(1)家庭中有兩個小孩;
(2)家庭中有三個小孩.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,且
,且![]() 對任意正整數
對任意正整數![]() 都成立,數列
都成立,數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在實數k,使數列![]() 是公比不為1的等比數列,且任意相鄰三項
是公比不為1的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列,若存在,求出所有k的值;若不存在,請說明理由;
按某順序排列后成等差數列,若存在,求出所有k的值;若不存在,請說明理由;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com