
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | ||
| C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1或$\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1或$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{3}$=1 |
分析 由當焦點在x軸上,設雙曲線方程,由離心率公式求得$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$,即可求得漸近線方程,由點到直線的距離公式即可求得a的值,求得雙曲線方程,同理當焦點在y軸上時,即可求得雙曲線方程.
解答 解:當焦點在x軸上,設雙曲線方程為$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0),
雙曲線的離心率為e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{7}}{2}$,
∴$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$,漸近線方程為y=±$\frac{\sqrt{3}}{2}$x,
由題意,頂點到漸近線的距離,$\frac{丨\frac{\sqrt{3}}{2}a丨}{\sqrt{\frac{3}{4}+1}}$=$\frac{2\sqrt{21}}{7}$,解得a=2,
∴∴b=$\sqrt{3}$,
∴雙曲線的方程為$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}=1$;
當焦點在y軸上,設雙曲線方程為$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),
漸近線方程為y=±$\frac{2\sqrt{3}}{3}$x,
由題意可知:頂點到漸近線的距離為$\frac{丨a丨}{\sqrt{\frac{4}{3}+1}}$=$\frac{2\sqrt{21}}{7}$,解得a=2,
∴b=$\sqrt{3}$,
∴雙曲線的方程為$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{3}=1$,
綜上可知:雙曲線的方程為:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}=1$或$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{3}=1$.
故選D.
點評 本題考查雙曲線的標準方程,雙曲線的簡單的幾何性質,漸近線方程及點到直線的距離公式,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 13 | B. | $\sqrt{151}$ | C. | 12$\sqrt{3}$ | D. | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如下圖,直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱C1的
如下圖,直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱C1的查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
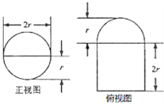 如圖是一個圓柱被一個平面截去一部分后與半球(半徑r=3)組成一個幾何體,該幾何圖體三視中的正視圖和俯視圖如圖所示,則該幾何體的表面積為( )
如圖是一個圓柱被一個平面截去一部分后與半球(半徑r=3)組成一個幾何體,該幾何圖體三視中的正視圖和俯視圖如圖所示,則該幾何體的表面積為( )| A. | 63π | B. | 80π | C. | 36+27π | D. | 36+45π |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com