已知正數等差數列{an}的前n項和為Sn,S12=24,則a6-a7最大值為( )
A.36
B.6
C.4
D.2
【答案】
分析:由正數等差數列{a
n}的前n項和為S
n,S
12=24,知a
6+a
7=4,由數列{a
n}是正數等差數列,a
6-a
7最大值要小于4,由此能求出結果.
解答:解:∵正數等差數列{a
n}的前n項和為S
n,S
12=24,
∴
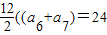
,
∴a
6+a
7=4,
∵數列{a
n}是正數等差數列,
∴a
6-a
7最大值要小于4,
故選D.
點評:本題考查等差數列的通項公式和前n項和公式的應用,是基礎題.解題時要認真審題,仔細解答.
