
【題目】已知函數![]() .
.
(Ⅰ)若關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)設函數![]() ,在(Ⅰ)的條件下,試判斷
,在(Ⅰ)的條件下,試判斷![]() 在
在![]() 上是否存在極值.若存在,判斷極值的正負;若不存在,請說明理由.
上是否存在極值.若存在,判斷極值的正負;若不存在,請說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)當
;(Ⅱ)當![]() 時,
時, ![]() 在
在![]() 上不存在極值;當
上不存在極值;當![]() 時,
時, ![]() 在
在![]() 上存在極值,且極值均為正.
上存在極值,且極值均為正.
【解析】試題分析:(1)不等式恒成立問題,一般先利用變量分離轉化為對應函數最值問題: ![]() 的最大值,利用導數研究函數
的最大值,利用導數研究函數![]() 最值,易得
最值,易得![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,因此
,因此![]() ,(2)即研究
,(2)即研究![]() 導函數的零點情況,先求導數,確定研究對象為
導函數的零點情況,先求導數,確定研究對象為![]() ,再求目標函數導數,確定單調性:先增后減,兩個端點值都小于零,討論最大值是否大于零,最后結合零點存在定理確定極值點個數.
,再求目標函數導數,確定單調性:先增后減,兩個端點值都小于零,討論最大值是否大于零,最后結合零點存在定理確定極值點個數.
試題解析:解:(Ⅰ)由![]() ,得
,得![]() .
.
即![]() 在
在![]() 上恒成立.
上恒成立.
設函數![]() ,
, ![]() .
.
則![]() .
.
∵![]() ,∴
,∴![]() .
.
∴當![]() 時,
時, ![]() .
.
∴![]() 在
在![]() 上單調遞減.
上單調遞減.
∴當![]() 時,
時, ![]() .
.
∴![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)![]() ,
, ![]() .
.
∴![]() .
.
設![]() ,則
,則![]() .
.
由![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
且![]() ,
, ![]() ,
, ![]() .
.
據(Ⅰ),可知![]() .
.
(ⅰ)當![]() ,即
,即![]() 時,
時, ![]() 即
即![]() .
.
∴![]() 在
在![]() 上單調遞減.
上單調遞減.
∴當![]() 時,
時, ![]() 在
在![]() 上不存在極值.
上不存在極值.
(ⅱ)當![]() ,即
,即![]() 時,
時,
則必定![]() ,使得
,使得![]() ,且
,且![]() .
.
當![]() 變化時,
變化時, ![]() ,
, ![]() ,
, ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 極小值 | ↗ | 極大值 | ↘ |
∴當![]() 時,
時, ![]() 在
在![]() 上的極值為
上的極值為![]() ,且
,且![]() .
.
∵![]() .
.
設![]() ,其中
,其中![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() ,當且僅當
,當且僅當![]() 時取等號.
時取等號.
∵![]() ,∴
,∴![]() .
.
∴當![]() 時,
時, ![]() 在
在![]() 上的極值
上的極值![]() .
.
綜上所述:當![]() 時,
時, ![]() 在
在![]() 上不存在極值;當
上不存在極值;當![]() 時,
時, ![]() 在
在![]() 上存在極值,且極值均為正.
上存在極值,且極值均為正.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的極值問題.
上的極值問題.


科目:高中數學 來源: 題型:
【題目】隨著智能手機的普及,使用手機上網成為了人們日常生活的一部分,很多消費者對手機流量的需求越來越大.長沙某通信公司為了更好地滿足消費者對流量的需求,準備推出一款流量包.該通信公司選了5個城市(總人數、經濟發展情況、消費能力等方面比較接近)采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價![]() :(單位:元/月)和購買人數
:(單位:元/月)和購買人數![]() (單位:萬人)的關系如表:
(單位:萬人)的關系如表:
![]()
(1)根據表中的數據,運用相關系數進行分析說明,是否可以用線性回歸模型擬合![]() 與
與![]() 的關系?并指出是正相關還是負相關;
的關系?并指出是正相關還是負相關;
(2)①求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②若該通信公司在一個類似于試點的城市中將這款流量包的價格定位25元/ 月,請用所求回歸方程預測長沙市一個月內購買該流量包的人數能否超過20 萬人.
參考數據:![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數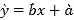 ,回歸直線方程
,回歸直線方程![]() ,
,
其中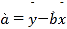 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+…+log3an,求數列![]() 的前n項和.
的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖因事故都受到不同程度的損壞,但可見部分如下,據此解答如下問題:
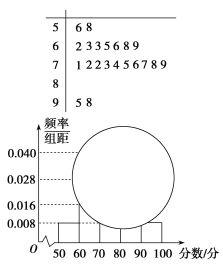
(1)求分數在[50,60)的頻率及全班人數;
(2)求分數在[80,90)的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(3)若規定:90分(包含90分)以上為優秀,現從分數在80分(包含80分)以上的試卷中任取兩份分析學生失分情況,求在抽取的試卷中至少有一份優秀的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“2019年”是一個重要的時間節點——中華人民共和國成立70周年,和全面建成小康社會的 關鍵之年.70年披荊斬棘,70年砥礪奮進,70年風雨兼程,70年滄桑巨變,勤勞勇敢的中國 人用自己的雙手創造了一項項輝煌的成績,取得了舉世矚目的成就.趁此良機,李明在天貓網店銷售“新中國成立70周年紀念冊”,每本紀念冊進價4元,物流費、管理費共為![]() 元/本,預計當每本紀念冊的售價為
元/本,預計當每本紀念冊的售價為![]() 元(
元(![]() 時,月銷售量為
時,月銷售量為![]() 千本.
千本.
(I)求月利潤![]() (千元)與每本紀念冊的售價X的函數關系式,并注明定義域:
(千元)與每本紀念冊的售價X的函數關系式,并注明定義域:
(II)當![]() 為何值時,月利潤
為何值時,月利潤![]() 最大?并求出最大月利潤.
最大?并求出最大月利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com