
 的最小值大于(m2-km+1)的最大值,所以分別求出最值,得到關于k的不等式求出解集即可.
的最小值大于(m2-km+1)的最大值,所以分別求出最值,得到關于k的不等式求出解集即可. ≥m2-km+1,則
≥m2-km+1,則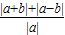 ≥
≥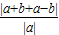 =2,設右邊=g(m)=m2-km+1為對稱軸為x=
=2,設右邊=g(m)=m2-km+1為對稱軸為x=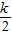 的開口向上的拋物線,由m∈[1,2],
的開口向上的拋物線,由m∈[1,2], ≤1即k≤2時,得到g(2)=4-2k+1為g(m)的最大值,即4-2k+1≤2,解得k≥
≤1即k≤2時,得到g(2)=4-2k+1為g(m)的最大值,即4-2k+1≤2,解得k≥ ,所以
,所以 ≤k≤2;
≤k≤2;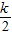 ≥2即k≥4時,g(1)=1-k+1為函數的最大值,即2-k≤2,得到k≥0,所以4≤k;
≥2即k≥4時,g(1)=1-k+1為函數的最大值,即2-k≤2,得到k≥0,所以4≤k;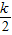 ≤2即2≤k≤4時,g(1)或g(2)為函數的最大值,
≤2即2≤k≤4時,g(1)或g(2)為函數的最大值, ≤k或k≥0,所以2≤k≤4.
≤k或k≥0,所以2≤k≤4. ,+∞)
,+∞) ,+∞)
,+∞)

 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com