
【題目】已知函數![]() .
.
(Ⅰ)求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)若對任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)當![]() 時,設函數
時,設函數![]() .證明:對于任意的
.證明:對于任意的![]() ,函數
,函數![]() 有且只有一個零點.
有且只有一個零點.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)見證明
(Ⅲ)見證明
【解析】
(I)求得切點坐標和斜率,由此求得切線方程.(II)將原不等式分離常數,得到![]() 恒成立,構造函數
恒成立,構造函數![]() ,利用導數求得函數
,利用導數求得函數![]() 的最大值,由此求得
的最大值,由此求得![]() 的取值范圍.(III)先求得
的取值范圍.(III)先求得![]() 的表達式,然后利用導數證得
的表達式,然后利用導數證得![]() 在
在![]() 上有一個零點.再利用導數證得
上有一個零點.再利用導數證得![]() 在
在![]() 上沒有零點,由此得證.
上沒有零點,由此得證.
解:(Ⅰ)已知函數![]() ,
,
可得![]() ,且
,且![]() ,
,
函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅱ)![]() 對任意
對任意![]() 恒成立,所以
恒成立,所以![]() .
.
令![]() ,則
,則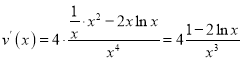
令![]() ,解得
,解得![]() .
.
當時![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞減.
上單調遞減.
所以![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() 的取值范圍為
的取值范圍為![]() .
.
(Ⅲ)證明:由已知![]() ,則
,則![]() .且可知
.且可知![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 有唯一實根.
有唯一實根.
當![]() 時,令
時,令![]() ,則
,則![]() .
.![]() ,
,![]() 在
在![]() 單調遞減;在
單調遞減;在![]() 單調遞增.所以
單調遞增.所以![]() .所以
.所以![]() 在
在![]() 沒有實根.
沒有實根.
綜上,對于任意的![]() ,函數
,函數![]() 有且只有一個零點.
有且只有一個零點.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是正方形,四邊形
是正方形,四邊形![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
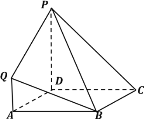
(Ⅰ)求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)已知點![]() 在棱
在棱![]() 上,且異面直線
上,且異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
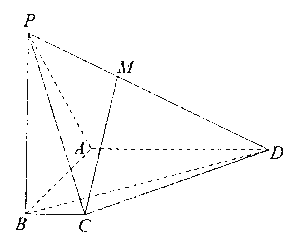
【題目】如圖,在四棱錐![]() 中:
中:![]() 底面ABCD,底面ABCD為梯形,
底面ABCD,底面ABCD為梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M為棱PD上的點。
,BC=1,M為棱PD上的點。
(Ⅰ)若![]() ,求證:CM∥平面PAB;
,求證:CM∥平面PAB;
(Ⅱ)求證:平面![]() 平面PAB;
平面PAB;
(Ⅲ)求直線BD與平面PAD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 與
與![]() 滿足的關系;
滿足的關系;
(2)當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(3)當![]() 時,對任意的
時,對任意的![]() ,總有
,總有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為我國數學家趙爽(約3世紀初)在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不相同,則不同的涂色方案共有( )
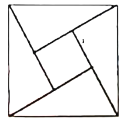
A.360種B.720種C.480種D.420種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知8件不同的產品中有3件次品,現對它們一一進行測試,直至找到所有次品.
(1)若恰在第2次測試時,找到第一件次品,第6次測試時,才找到最后一件次品,則共有多少種不同的測試方法?
(2)若至多測試5次就能找到所有次品,則共有多少種不同的測試方法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右頂點是雙曲線
的左右頂點是雙曲線![]() 的頂點,且橢圓
的頂點,且橢圓![]() 的上頂點到雙曲線
的上頂點到雙曲線![]() 的漸近線的距離為
的漸近線的距離為![]() 。
。
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com