
【題目】已知f(x)= ![]() ,g(x)=|x﹣2|,則下列結論正確的是( )
,g(x)=|x﹣2|,則下列結論正確的是( )
A.h(x)=f(x)+g(x)是偶函數
B.h(x)=f(x)?g(x)是奇函數
C.h(x)= ![]() 是偶函數
是偶函數
D.h(x)= ![]() 是奇函數
是奇函數
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2﹣(2a﹣1)x﹣lnx.
(1)當a>0時,求函數f(x)的單調遞增區間;
(2)當a<0時,求函數f(x)在 ![]() 上的最小值;
上的最小值;
(3)記函數y=f(x)的圖象為曲線C,設點A(x1 , y1),B(x2 , y2)是曲線C上的不同兩點,點M為線段AB的中點,過點M作x軸的垂直交曲線C于點N,判斷曲線C在點N處的切線是否平行于直線AB,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義下凸函數如下:設f(x)為區間I上的函數,若對任意的x1 , x2∈I總有f( ![]() )≥
)≥ ![]() ,則稱f(x)為I上的下凸函數,某同學查閱資料后發現了下凸函數有如下判定定理和性質定理: 判定定理:f(x)為下凸函數的充要條件是f″(x)≥0,x∈I,其中f″(x)為f(x)的導函數f′(x)的導數.
,則稱f(x)為I上的下凸函數,某同學查閱資料后發現了下凸函數有如下判定定理和性質定理: 判定定理:f(x)為下凸函數的充要條件是f″(x)≥0,x∈I,其中f″(x)為f(x)的導函數f′(x)的導數.
性質定理:若函數f(x)為區間I上的下凸函數,則對I內任意的x1 , x2 , …,xn , 都有 ![]() ≥f(
≥f( ![]() ).
).
請問:在△ABC中,sinA+sinB+sinC的最大值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某氣象站觀測點記錄的連續4天里,AQI指數M與當天的空氣水平可見度y(單位cm)的情況如下表1:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
哈爾濱市某月AQI指數頻數分布如下表2:
M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設x= ![]() ,根據表1的數據,求出y關于x的回歸方程; (參考公式:
,根據表1的數據,求出y關于x的回歸方程; (參考公式: ![]() ;其中
;其中 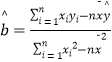 ,
, ![]() )
)
(2)小張開了一家洗車店,經統計,當M不高于200時,洗車店平均每天虧損約2000元;當M在200至400時,洗車店平均每天收入約4000元;當M大于400時,洗車店平均每天收入約7000元;根據表2估計小張的洗車店該月份平均每天的收入.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點O為極點,x軸為正半軸為極軸,建立極坐標系.設曲線C: ![]() (α為參數);直線l:ρ(cosθ+sinθ)=4.
(α為參數);直線l:ρ(cosθ+sinθ)=4.
(Ⅰ)寫出曲線C的普通方程和直線l的直角坐標方程;
(Ⅱ)求曲線C上的點到直線l的最大距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在圓心角為![]() ,半徑為
,半徑為![]() 的扇形鐵皮上截取一塊矩形材料
的扇形鐵皮上截取一塊矩形材料![]() ,其中點
,其中點![]() 為圓心,點
為圓心,點![]() 在圓弧上,點
在圓弧上,點![]() 在兩半徑上,現將此矩形鐵皮
在兩半徑上,現將此矩形鐵皮![]() 卷成一個以
卷成一個以![]() 為母線的圓柱形鐵皮罐的側面(不計剪裁和拼接損耗),設矩形的邊長
為母線的圓柱形鐵皮罐的側面(不計剪裁和拼接損耗),設矩形的邊長![]() ,圓柱形鐵皮罐的容積為
,圓柱形鐵皮罐的容積為![]() .
.

(1)求圓柱形鐵皮罐的容積![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)當![]() 為何值時,才使做出的圓柱形鐵皮罐的容積
為何值時,才使做出的圓柱形鐵皮罐的容積![]() 最大?最大容積是多少? (圓柱體積公式:
最大?最大容積是多少? (圓柱體積公式:![]() ,
,![]() 為圓柱的底面枳,
為圓柱的底面枳,![]() 為圓柱的高)
為圓柱的高)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,AC是弦,∠BAC的平分線AD交圓O于點D,DE⊥AC,交AC的延長線于點E,OE交AD于點F. 
(1)求證:DE是圓O的切線;
(2)若∠CAB=60°,⊙O的半徑為2,EC=1,求DE的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位員工![]() 人參加“學雷鋒”志愿活動,按年齡分組:第
人參加“學雷鋒”志愿活動,按年齡分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
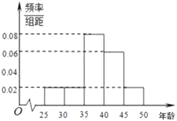
(1)下表是年齡的頻率分布表,求正整數![]() 的值;
的值;
區間 |
|
|
|
|
|
人數 |
|
|
|
|
|
(2)現在要從年齡較小的第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,年齡在第
人,年齡在第![]() 組抽取的員工的人數分別是多少?
組抽取的員工的人數分別是多少?
(3)在(2)的前提下,從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加社區宣傳交流活動,求至少有
人參加社區宣傳交流活動,求至少有![]() 人年齡在第
人年齡在第![]() 組的概率.
組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角△ABC中,AB⊥BC,D為BC邊上異于B、C的一點,以AB為直徑作⊙O,并分別交AC,AD于點E,F.
(Ⅰ)證明:C,E,F,D四點共圓;
(Ⅱ)若D為BC的中點,且AF=3,FD=1,求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com