
【題目】如圖,在四棱柱![]() 為長方體,點
為長方體,點![]() 是
是![]() 上的一點.
上的一點.
(1)若![]() 為
為![]() 的中點,當
的中點,當![]() 為何值時,平面
為何值時,平面![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() ,當
,當![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成角的正弦值是否存在最大值?若存在,求出
所成角的正弦值是否存在最大值?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.

【答案】(1)![]() (2)
(2)![]() 時,
時, ![]() 取得最大值1.
取得最大值1.
【解析】試題分析:(1)要使平面![]() 平面
平面![]() ,只需
,只需![]() 平面
平面![]() .,只需
.,只需![]() ,只需
,只需![]() ,因為
,因為![]() 為
為![]() 的中點,所以
的中點,所以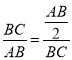 ,所以
,所以![]() ;(2)建立空間直角坐標系,寫出直線與平面所成角的正弦,利用二次函數(shù)求其最大值即可.
;(2)建立空間直角坐標系,寫出直線與平面所成角的正弦,利用二次函數(shù)求其最大值即可.
試題解析:(1)要使平面![]() 平面
平面![]() ,只需
,只需![]() 平面
平面![]() .
.
因為四棱柱![]() 為長方體,
為長方體,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又因為![]() ,所以只需
,所以只需![]() ,
,
只需![]() ,只需
,只需![]() ∽
∽![]() ,
,
因為![]() ,所以只需
,所以只需![]() ,
,
因為![]() 為
為![]() 的中點,所以
的中點,所以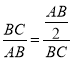 ,所以
,所以![]() .
.
所以當![]() 時,平面
時,平面![]() 平面
平面![]() .
.
(2)存在.理由如下:建立如圖所示的空間直角坐標系![]() ,
,
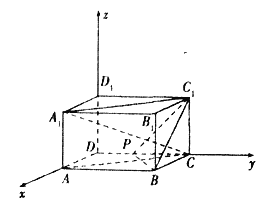
則![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,則
,則![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,
所以![]() ,取
,取![]() ,則
,則![]() ,
,
所以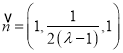 ,
,
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則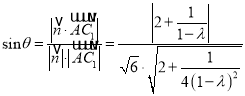
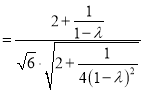
令![]() ,則
,則![]() ,
, ![]() ,
,
所以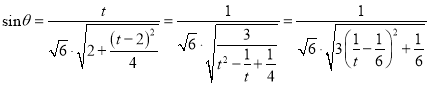
所以當![]() ,即
,即![]() ,
,![]() 時,
時, ![]() 取得最大值1.
取得最大值1.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數(shù)學 來源: 題型:
【題目】設正項數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() ,
, ![]() ,各項均為正數(shù)的等比數(shù)列
,各項均為正數(shù)的等比數(shù)列![]() 滿足
滿足![]() .
.
(Ⅰ)求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(Ⅱ)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() .若對任意
.若對任意![]() ,
, ![]() ,均有
,均有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義在R上的函數(shù)f(x),g(x)滿足:對于任意的x,都有f(﹣x)+f(x)=0,g(x)=g(|x|).當x<0時,f′(x)<0,g′(x)>0,則當x>0時,有( )
A.f'(x)>0,g′(x)>0
B.f′(x)<0,g′(x)<0
C.f′(x)<0,g′(x)>0
D.f′(x)>0,g′(x)<0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)=xlnx,g(x)= ![]() ,直線l:y=(k﹣3)x﹣k+2
,直線l:y=(k﹣3)x﹣k+2
(1)函數(shù)f(x)在x=e處的切線與直線l平行,求實數(shù)k的值
(2)若至少存在一個x0∈[1,e]使f(x0)<g(x0)成立,求實數(shù)a的取值范圍
(3)設k∈Z,當x>1時f(x)的圖象恒在直線l的上方,求k的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系中,已知射線OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).過點P(1,0)作直線分別交射線OA,OB于點A,B.
(1)當AB的中點在直線x﹣2y=0上時,求直線AB的方程;
(2)當△AOB的面積取最小值時,求直線AB的方程.
(3)當PAPB取最小值時,求直線AB的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在R上定義運算:xy=x(1﹣y),若不等式(x﹣a)(x﹣b)>0的解集是(2,3),則a+b的值為( )
A.1
B.2
C.4
D.8
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)f(x)滿足:在定義域D內存在實數(shù)x0 , 使得f(x0+1)=f(x0)+f(1)成立,則稱函數(shù)f(x)為“1的飽和函數(shù)”.給出下列四個函數(shù):①f(x)= ![]() ;②f(x)=2x;③f(x)=lg(x2+2);④f(x)=cos(πx).其中是“1的飽和函數(shù)”的所有函數(shù)的序號為( )
;②f(x)=2x;③f(x)=lg(x2+2);④f(x)=cos(πx).其中是“1的飽和函數(shù)”的所有函數(shù)的序號為( )
A.①③
B.②④
C.①②
D.③④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】數(shù)列{an}是首項a1=4的等比數(shù)列,且S3 , S2 , S4成等差數(shù)列,
(1)求數(shù)列{an}的通項公式;
(2)若bn=log2|an|,設Tn為數(shù)列 ![]() 的前n項和,若Tn≤λbn+1對一切n∈N*恒成立,求實數(shù)λ的最小值.
的前n項和,若Tn≤λbn+1對一切n∈N*恒成立,求實數(shù)λ的最小值.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com