
【題目】如圖所示,正方體![]() 的棱長為
的棱長為![]() ,
, ![]() ,
, ![]() 分別是棱
分別是棱![]() ,
, ![]() 的中點,過直線
的中點,過直線![]() ,
, ![]() 的平面分別與棱
的平面分別與棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,設
,設![]() ,
, ![]() ,給出以下四個命題:
,給出以下四個命題:
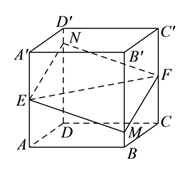
①四邊形![]() 為平行四邊形;
為平行四邊形;
②若四邊形![]() 面積
面積![]() ,
, ![]() ,則
,則![]() 有最小值;
有最小值;
③若四棱錐![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 是常函數;
是常函數;
④若多面體![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 為單調函數.
為單調函數.
其中假命題為( ).
A. ① B. ② C. ③ D. ④
科目:高中數學 來源: 題型:
【題目】在平面直角坐標平面中, ![]() 的兩個頂點為
的兩個頂點為![]() ,平面內兩點
,平面內兩點![]() 、
、![]() 同時滿足:①
同時滿足:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)求頂點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,直線
,直線![]() 與點
與點![]() 的軌跡
的軌跡![]() 相交弦分別為
相交弦分別為![]() ,設弦
,設弦![]() 的中點分別為
的中點分別為![]() .
.
①求四邊形![]() 的面積
的面積![]() 的最小值;
的最小值;
②試問:直線![]() 是否恒過一個定點?若過定點,請求出該定點,若不過定點,請說明理由.
是否恒過一個定點?若過定點,請求出該定點,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接世博會,某旅游區提倡低碳生活,在景區提供自行車出租。該景區有50輛自行車供游客租賃使用,管理這些自行車的費用是每日115元。根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超出6元,則每超過1元,租不出的自行車就增加3輛。為了便于結算,每輛自行車的日租金x(元)只取整數,并且要求出租自行車一日的總收入必須高于這一日的管理費用,用y(元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費用后的所得).
(1)求函數![]() 的解析式及其定義域;
的解析式及其定義域;
(2)試問當每輛自行車的日租金定為多少元時,才能使一日的凈收入最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() lnx-x+
lnx-x+![]() ,其中a>0.
,其中a>0.
(1)若f(x)在(0,+∞)上存在極值點,求a的取值范圍;
(2)設a∈(1,e],當x1∈(0,1),x2∈(1,+∞)時,記f(x2)-f(x1)的最大值為M(a).那么M(a)是否存在最大值?若存在,求出其最大值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() ,且點
,且點![]() 到橢圓C的兩焦點的距離之和為
到橢圓C的兩焦點的距離之和為![]() .
.

(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ) 若![]() ,
,![]() 是橢圓
是橢圓![]() 上的兩個點,線段
上的兩個點,線段![]() 的中垂線
的中垂線![]() 的斜率為
的斜率為![]() ,且直線
,且直線![]() 與
與![]() 交于點
交于點![]() ,求證:點
,求證:點![]() 在直線
在直線![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構為了了解各年齡層對高考改革方案的關注程度,隨機選取了200名年齡在![]() 內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分第一~五組區間分別為
內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分第一~五組區間分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
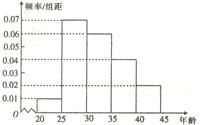
(1)求選取的市民年齡在![]() 內的人數;
內的人數;
(2)若從第3,4組用分層抽樣的方法選取5名市民進行座談,再從中選取2人在座談會中作重點發言,求作重點發言的市民中至少有一人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
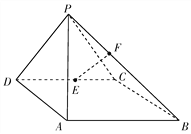
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定點![]() 的位置,使得直線
的位置,使得直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com