
【題目】已知函數f(x)=
(e為自然對數的底數),則f(e)=________,函數y=f(f(x))-1的零點個數為________.
【答案】 1 3
【解析】f(e)=lne=1;
函數y=f(f(x))-1的零點個數為方程f(f(x))=1的根的個數,則
①由ln x=1(x≥1),得x=e,于是f(x)=e,則由ln x=e(x≥1),得x=ee;或由ef(|x|+1)=e(x<1),得f(|x|+1)=1,所以ln(|x|+1)=1,解得x=e-1(舍去)或x=1-e;
②由ef(|x|+1)=1(x<1),得f(|x|+1)=0,所以ln(|x|+1)=0,解得x=0,所以f(x)=0,只有ln x=0(x≥1),解得x=1.
綜上可知函數y=f(f(x))-1有x=ee,1-e,1共3個零點.
答案:1 3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,正方體![]() 的棱長為
的棱長為![]() ,
, ![]() ,
, ![]() 分別是棱
分別是棱![]() ,
, ![]() 的中點,過直線
的中點,過直線![]() ,
, ![]() 的平面分別與棱
的平面分別與棱![]() ,
, ![]() 交于
交于![]() ,
, ![]() ,設
,設![]() ,
, ![]() ,給出以下四個命題:
,給出以下四個命題:
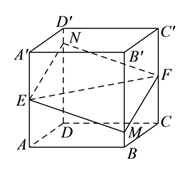
①四邊形![]() 為平行四邊形;
為平行四邊形;
②若四邊形![]() 面積
面積![]() ,
, ![]() ,則
,則![]() 有最小值;
有最小值;
③若四棱錐![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 是常函數;
是常函數;
④若多面體![]() 的體積
的體積![]() ,
, ![]() ,則
,則![]() 為單調函數.
為單調函數.
其中假命題為( ).
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別是240,160,160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動。
(1)應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人?
(2)設抽出的7名同學分別用A,B,C,D,E,F,G表示,現從中隨機抽取2名同學承擔敬老院的衛生工作,求事件M“抽取的2名同學來自同一年級”發生的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位學生參加數學競賽培訓.現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取![]() 次.記錄如下:
次.記錄如下:
甲: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
乙: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(![]() )用莖葉圖表示這兩組數據.
)用莖葉圖表示這兩組數據.
(![]() )現要從中選派一人參加數學競賽,從統計學的角度考慮,你認為派哪位學生參加合適?請說明理由.
)現要從中選派一人參加數學競賽,從統計學的角度考慮,你認為派哪位學生參加合適?請說明理由.
(![]() )若將頻率視為概率,對甲同學在今后的三次數學競賽成績進行預測,記這
)若將頻率視為概率,對甲同學在今后的三次數學競賽成績進行預測,記這![]() 次成績中高于
次成績中高于![]() 分的次數為
分的次數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校某研究性學習小組在對學生上課注意力集中情況的調查研究中,發現其在40分鐘的一節課中,注意力指數y與聽課時間x(單位:分鐘)之間的關系滿足如圖所示的圖象,當x∈(0,12]時,圖象是二次函數圖象的一部分,其中頂點A(10,80),過點B(12,78);當x∈[12,40]時,圖象是線段BC,其中C(40,50).根據專家研究,當注意力指數大于62時,學習效果最佳.
(1)試求y=f(x)的函數關系式;
(2)教師在什么時段內安排內核心內容,能使得學生學習效果最佳?請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,圓
,圓![]() :
:![]() ,動圓
,動圓![]() 與圓
與圓![]() 外切并且與圓
外切并且與圓![]() 內切,圓心
內切,圓心![]() 軌跡為曲線
軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() 是曲線
是曲線![]() 上關于
上關于![]() 軸對稱的兩點,點
軸對稱的兩點,點![]() ,直線
,直線![]() 交曲線
交曲線![]()
于另一點![]() ,求證:直線
,求證:直線![]() 過定點,并求該定點的坐標.
過定點,并求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列{an}是公差為2的等差數列,數列{bn}滿足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求數列{an},{bn}的通項公式;
(2)設數列{cn}滿足![]() ,數列{cn}的前n項和為Tn,若不等式(-1)nλ<Tn+
,數列{cn}的前n項和為Tn,若不等式(-1)nλ<Tn+![]() 對一切n∈N*恒成立,求實數λ的取值范圍.
對一切n∈N*恒成立,求實數λ的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com