
【題目】在“創文創衛”活動中,某機構為了解一小區成年居民“吸煙與性別”是否有關.從該小區中隨機抽取200位成年居民,得到下邊列聯表:已知在全部200人中隨機抽取1人,抽到不吸煙的概率為0.75.
吸煙 | 不吸煙 | 合計 | |
男 | 40 | ||
女 | 90 | ||
合計 | 200 |
(1)補充上面的列聯表,并判斷:能否有99.9%的把握認為“吸煙與性別”有關;
(2)用分層抽樣的方法從吸煙居民中選5人出來,然后再從中抽2人出來,給小區居民談談吸煙的危害性,求恰好抽到“一男一女”的概率.
參考公式: 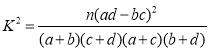 .
.
參考數據:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)列聯表詳見解析,有99.9%的把握認為“吸煙與性別”有關;(2)![]()
【解析】
(1)由條件填寫列聯表,然后計算![]() 和10.828比較大小,做出判斷;
和10.828比較大小,做出判斷;
(2)分層抽樣可知,男生中選4人,女生中選1人,然后一一列舉出所有的基本事件和滿足條件的基本事件的個數,求概率.
(1)由條件可知![]() 人,
人,
所以男生中不吸煙的人數為![]() 人,
人,
女生中吸煙人數為![]() 人,
人,
列聯表如下:
吸煙 | 不吸煙 | 合計 | |
男 | 40 | 60 | 100 |
女 | 10 | 90 | 100 |
合計 | 50 | 150 | 200 |
 ,
,
![]() 有99.9%的把握認為“吸煙與性別”有關;
有99.9%的把握認為“吸煙與性別”有關;
(2)由分層抽樣可知,男生中選4人,女生中選1人,
男生設為![]() ,女生設為
,女生設為![]() ,
,
則任選2人的基本事件為![]() ,
,![]() ,
,
![]() ,共10個基本事件,
,共10個基本事件,
其中恰好抽到“一男一女”的共有![]() 共4個基本事件,
共4個基本事件,
則恰好抽到“一男一女”的概率是![]() .
.


 互動英語系列答案
互動英語系列答案 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案科目:高中數學 來源: 題型:
【題目】設數列![]()
![]() 是公差不為零等差數列,滿足
是公差不為零等差數列,滿足![]() ;數列
;數列![]()
![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)在![]() 和
和![]() 之間插入1個數
之間插入1個數![]() ,使
,使![]() 成等差數列;在
成等差數列;在![]() 和
和![]() 之間插入2個數
之間插入2個數![]() ,使
,使![]() 成等差數列;……;在
成等差數列;……;在![]() 和
和![]() 之間插入
之間插入![]() 個數
個數![]() ,使
,使![]() 成等差數列,
成等差數列,
(i)求![]() ;
;
(ii)是否存在正整數![]() ,使
,使![]() 成立?若存在,求出所有的正整數對
成立?若存在,求出所有的正整數對![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究在
兩點,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得可
,使得可![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標,若不存在,請說明理由?
的坐標,若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(x>0).
,(x>0).
(1)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(2)是否存在實數a,b(a<b),使得函數y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(3)若存在實數a,b(a<b),使得函數y=f(x)的定義域為[a,b]時,值域為[ma,mb](m≠0),求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校成立了數學、英語、音樂3個課外興趣小組,3個小組分別有39、32、33個成員,一些成員參加了不止一個小組,具體情況如圖所示.
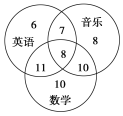
現隨機選取一個成員,他屬于至少2個小組的概率是________,他屬于不超過2個小組的概率是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知i為虛數單位,a為實數,復數z=(1﹣2i)(a+i)在復平面內對應的點為M,則![]() “”是“點M在第四象限”的( )
“”是“點M在第四象限”的( )
A.充分而不必要條件
B.必要而不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com