Question

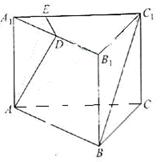
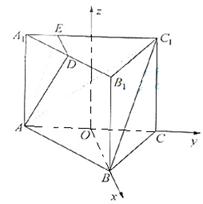
如圖4，在正三棱柱中，

D是的中點，點E在上，且。

（I）                    證明平面平面

（II）                  求直線和平面所成角的正弦值。

Answer 1

（Ⅰ）略（Ⅱ）

解析:

（I） 如圖所示，由正三棱柱的性質知平面

又DE平面ABC，所以DEAA.

而DEAE。AAAE=A  所以DE平面AC CA，又DE平面ADE，故平面ADE平面AC CA。

（2）解法1  如圖所示，設F使AB的中點，連接DF、DC、CF，由正三棱柱ABC- ABC的性質及D是AB的中點知ABCD，  ABDF

又CDDF=D，所以AB平面CDF，

而AB∥AB，所以

AB平面CDF，又AB平面ABC，故

平面AB C平面CDF。

過點D做DH垂直CF于點H，則DH平面AB C。

連接AH，則HAD是AD和平面ABC所成的角。

由已知AB=A A，不妨設A A=，則AB=2，DF=，D C=，

CF=，AD==，DH==—，

所以 sinHAD==。

即直線AD和平面AB C所成角的正弦值為。

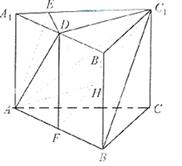
解法2  如圖所示，設O使AC的中點，以O為原點建立空間直角坐標系，不妨設

A A=，則AB=2，相關各點的坐標分別是

A(0,-1,0)， B（，0，0），  C（0，1，），  D（，-，）。

易知=(，1，0)， =(0，2，)， =(，-，）

設平面ABC的法向量為n=（x，y，z）,則有

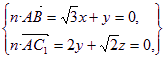
解得x=-y， z=-，

故可取n=(1，-，)。

所以，(n·)===。

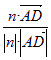由此即知，直線AD和平面AB C所成角的正弦值為。