
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() .
.
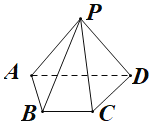
(1)在線段PA上找一點E,使得![]() 平面PCD,并證明;
平面PCD,并證明;
(2)在(1)的條件下,若![]() ,求點E到平面PCD的距離.
,求點E到平面PCD的距離.
【答案】(1)E是線段PA的中點,證明詳見解析;(2)![]() .
.
【解析】
(1)當E是線段PA的中點,利用中位線可得![]() ,再由平行四邊形可得
,再由平行四邊形可得![]() ,則平面
,則平面![]() 平面PCD,進而求證即可;
平面PCD,進而求證即可;
(2)由題可得![]() 平面ABCD,利用等體積法可得
平面ABCD,利用等體積法可得![]() ,即可求得點O到平面PCD的距離為d,進而由(1)的平行關系求解即可
,即可求得點O到平面PCD的距離為d,進而由(1)的平行關系求解即可
(1)當E是線段PA的中點,
證明:記O為AD的中點,連接BE,OE,OB,
∵O是AD的中點,∴![]() ,
,
又![]() 平面PCD,
平面PCD,![]() 平面PCD,
平面PCD,
∴![]() 平面PCD,
平面PCD,
又∵底面ABCD是直角梯形,![]() ,
,
∴![]() ,
,
又![]() 平面PCD,
平面PCD,![]() 平面PCD,
平面PCD,
∴![]() 平面PCD,
平面PCD,
∵![]() 平面OBE,
平面OBE,![]() 平面OBE,
平面OBE,![]() ,
,
∴平面![]() 平面PCD,
平面PCD,
又![]() 平面OBE,
平面OBE,
∴![]() 平面PCD
平面PCD
(2)解:∵連接PO,CO,
![]() 平面
平面![]() 平面ABCD,
平面ABCD,![]() ,
,
∴![]() ,∴
,∴![]() 平面ABCD,
平面ABCD,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,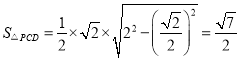 ,
,
設點O到平面PCD的距離為d,由等體積法可得![]()
即![]() ,解得
,解得![]()
由(1)知點O到平面PCD的距離等于點E到平面PCD的距離,
故點E到平面PCD的距離為![]()


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 經過點
經過點![]() ,右焦點到直線
,右焦點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)定義![]() 為
為![]() ,
,![]() 兩點所在直線的斜率,若四邊形
兩點所在直線的斜率,若四邊形![]() 為橢圓的內接四邊形,且
為橢圓的內接四邊形,且![]() ,
,![]() 相交于原點
相交于原點![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟水平及個人消費能力的提升,我國居民對精神層面的追求愈加迫切,如圖是2007年到2017年我國城鎮居民教育、文化、服務人均消費支出同比增速的折線圖,圖中顯示2007年的同比增速為10%, 即2007年與2006年同時期比較2007年的人均消費支出費用是2006年的1.1倍.則下列表述中正確的是( )
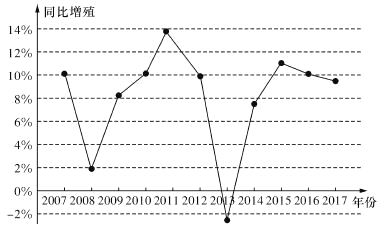
A.2007年到2017年,同比增速的中位數約為10%
B.2007年到2017年,同比增速的極差約為12%
C.2011年我國城鎮居民教育、文化、服務人均消費支出的費用最高
D.2007年到2017年,我國城鎮居民教育、文化、服務人均消費支出的費用逐年增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上一點,且
上一點,且![]() .三棱錐
.三棱錐![]() 的各個頂點都在球
的各個頂點都在球![]() 表面上,過點
表面上,過點![]() 作球
作球![]() 的截面,若所得截面圓的面積的最大值與最小值之差為
的截面,若所得截面圓的面積的最大值與最小值之差為![]() ,則球
,則球![]() 的表面積為( )
的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓上存在一點
,且橢圓上存在一點![]() ,滿足
,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
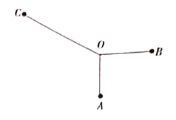
【題目】如圖,某同學在素質教育基地通過自己設計、選料、制作,打磨出了一個作品,作品由三根木棒![]() ,
,![]() ,
,![]() 組成,三根木棒有相同的端點
組成,三根木棒有相同的端點![]() (粗細忽略不計),且
(粗細忽略不計),且![]() 四點在同一平面內,
四點在同一平面內,![]()
![]() ,
,![]() ,木棒
,木棒![]() 可繞點O任意旋轉,設BC的中點為D.
可繞點O任意旋轉,設BC的中點為D.
(1)當![]() 時,求OD的長;
時,求OD的長;
(2)當木棒OC繞點O任意旋轉時,求AD的長的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
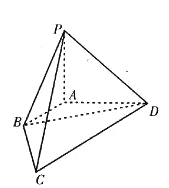
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com