
【題目】已知函數(shù)![]() (
(![]() 且
且![]() ,e為自然對數(shù)的底數(shù).)
,e為自然對數(shù)的底數(shù).)
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 只有一個零點,求a的值.
只有一個零點,求a的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)代入![]() ,得
,得![]() ,所以
,所以![]() ,求出
,求出![]() ,由直線方程的點斜式,即可得到切線方程;
,由直線方程的點斜式,即可得到切線方程;
(2)分![]() 和
和![]() 兩種情況,考慮函數(shù)
兩種情況,考慮函數(shù)![]() 的最小值,令最小值等于0,即可得到a的值.
的最小值,令最小值等于0,即可得到a的值.
解:(1)當![]() 時,
時,![]() ,
,![]()
![]() ,
,![]() ,∴切線方程為
,∴切線方程為![]() ;
;
(2)![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,
1)當![]() 時,
時,![]() ,
,
x |
|
|
|
| - | 0 | + |
|
| 極小值 |
|
所以當![]() 時,
時,![]() 有最小值,
有最小值,![]() .
.
因為函數(shù)![]() 只有一個零點,且當
只有一個零點,且當![]() 和
和![]() 時,都有
時,都有![]() ,
,
所以![]() ,即
,即![]() ,
,
因為當![]() 時,
時,![]() ,所以此方程無解.
,所以此方程無解.
2)當![]() 時,
時,![]() ,
,
x |
|
|
|
| - | 0 | + |
|
| 極小值 |
|
所以當![]() 時,
時,![]() 有最小值,
有最小值,![]() .
.
因為函數(shù)![]() 只有一個零點,且當
只有一個零點,且當![]() 和
和![]() 時,都有
時,都有![]() ,
,
所以![]() ,即
,即![]() (
(![]() )(*),
)(*),
設![]() (
(![]() ),則
),則![]() ,
,
令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以當![]() 時,
時,![]() ,
,
所以方程(*)有且只有一解![]() .
.
綜上,![]() 時函數(shù)
時函數(shù)![]() 只有一個零點.
只有一個零點.


 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,左頂點為
,左頂點為![]() ,離心率為
,離心率為![]() ,點
,點![]() 是橢圓上的動點,
是橢圓上的動點,![]() 的面積的最大值為
的面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設經(jīng)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() ,線段
,線段![]() 的中垂線為
的中垂線為![]() .若直線
.若直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,與直線
,與直線![]() 相交于點
相交于點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
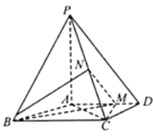
【題目】如圖,四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,
上一點,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離;
的距離;
(3)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在梯形ABCD中,DC∥AB,DC⊥CB,E是AB的中點,且AB=2BC=2CD=4(如圖所示),將△ADE沿DE翻折,使AB=2(如圖所示),F是線段AD上一點,且AF=2DF.
(Ⅰ)求四棱錐A-BCDE的體積;
(Ⅱ)在線段BE上是否存在一點G,使EF∥平面ACG?若存在,請指出點G的位置,并證明你的結論;若不存在,請說明理由.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校有初級教師21人,中級教師14人,高級教師7人,現(xiàn)采用分層抽樣的方法從這些教師中抽取6人對績效工資情況進行調(diào)查.
(1)求應從初級教師,中級教師,高級教師中分別抽取的人數(shù);
(2)若從抽取的6名教師中隨機抽取2名做進一步數(shù)據(jù)分析,求抽取的2名均為初級教師的概率。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,AD=DC=AP=2,AB=1,點E為棱PC的中點.
,AD=DC=AP=2,AB=1,點E為棱PC的中點.
(1)證明:BE⊥DC;
(2)若F為棱PC上一點,滿足BF⊥AC,求二面角F-AB-P的余弦值.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】觀察下表:
1,2,3,
4,5,6,7,8,
9,10,11,12,13,14,15,
16,17,18,19,20,21,22,23,24,
……
問:(1)此表第![]() 行的第一個數(shù)與最后一個數(shù)分別是多少?
行的第一個數(shù)與最后一個數(shù)分別是多少?
(2)此表第![]() 行的各個數(shù)之和是多少?
行的各個數(shù)之和是多少?
(3)2019是第幾行的第幾個數(shù)?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】暑假期間,某旅行社為吸引中學生去某基地參加夏令營,推出如下收費標準:若夏令營人數(shù)不超過30,則每位同學需交費用600元;若夏令營人數(shù)超過30,則營員每多1人,每人交費額減少10元(即:營員31人時,每人交費590元,營員32人時,每人交費580元,以此類推),直到達到滿額70人為止.
(1)寫出夏令營每位同學需交費用![]() (單位:元)與夏令營人數(shù)
(單位:元)與夏令營人數(shù)![]() 之間的函數(shù)關系式;
之間的函數(shù)關系式;
(2)當夏令營人數(shù)為多少時,旅行社可以獲得最大收入?最大收入是多少?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com