
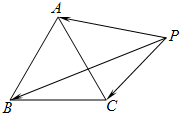
 如圖,△ABC是邊長為1的正三角形,點P在△ABC所在的平面內,且
如圖,△ABC是邊長為1的正三角形,點P在△ABC所在的平面內,且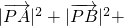
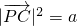 (a為常數).下列結論中,正確的是
(a為常數).下列結論中,正確的是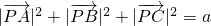 化為關于x、y、a的式子,化簡整理可得x2+(y-
化為關于x、y、a的式子,化簡整理可得x2+(y- )2=
)2= (a-1),討論a的取值范圍,可得當a>1時方程表示以點(0,
(a-1),討論a的取值范圍,可得當a>1時方程表示以點(0, )為圓心,半徑r=
)為圓心,半徑r=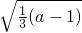 的圓,滿足條件的點P有無數個,可知只有C項符合題意.
的圓,滿足條件的點P有無數個,可知只有C項符合題意.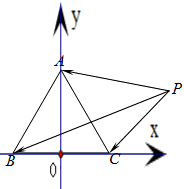 解:以BC所在直線為x軸,BC中點為原點,建立直角坐標系,如圖所示
解:以BC所在直線為x軸,BC中點為原點,建立直角坐標系,如圖所示 ,0),B(
,0),B( ,0),C(0,
,0),C(0, ),設P(x,y),可得
),設P(x,y),可得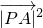 =x2+(y-
=x2+(y- )2,
)2,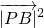 =(x+
=(x+ )2+y2,
)2+y2, =(x-
=(x- )2+y2
)2+y2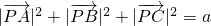
 )2+(x+
)2+(x+ )2+y2+(x-
)2+y2+(x- )2+y2=a
)2+y2=a y+
y+ -a=0,即x2+y2-
-a=0,即x2+y2- y+
y+ -
- =0
=0 )2=
)2= (a-1)…(1)
(a-1)…(1) ),恰好是正三角形的重心;
),恰好是正三角形的重心; )為圓心,半徑為
)為圓心,半徑為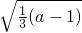 的圓
的圓

科目:高中數學 來源: 題型:
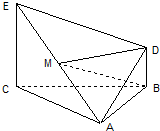 如圖:△ABC是邊長為2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.
如圖:△ABC是邊長為2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•徐州模擬)如圖,△ABC是邊長為2
(2012•徐州模擬)如圖,△ABC是邊長為2| 3 |
| AP |
| BP |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•江蘇三模)如圖,△ABC是邊長為2
(2012•江蘇三模)如圖,△ABC是邊長為2| 3 |
| AP |
| BP |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•普陀區二模)如圖,△ABC是邊長為1的正三角形,點P在△ABC所在的平面內,且|
(2013•普陀區二模)如圖,△ABC是邊長為1的正三角形,點P在△ABC所在的平面內,且|| PA |
| PB |
| PC |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com