
函數(shù)
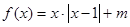
(1)設(shè)函數(shù)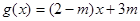 ,若方程
,若方程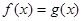 在
在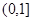 上有且僅一個實根,求實數(shù)
上有且僅一個實根,求實數(shù) 的取值范圍;
的取值范圍;
(2)當(dāng)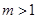 時,求函數(shù)
時,求函數(shù)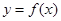 在
在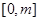 上的最大值.
上的最大值.
(1)實數(shù) 的取值范圍
的取值范圍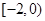
(2)當(dāng)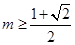 時,
時,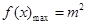 ,當(dāng)
,當(dāng)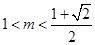 時,
時,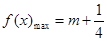
解析試題分析:(1)由二次方程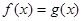 在
在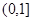 上有且僅一個實根,說明
上有且僅一個實根,說明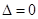 且根在
且根在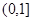 上或一根在
上或一根在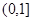 上一根不在
上一根不在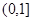 上兩種情況,由以上情況列出相應(yīng)關(guān)系式求實數(shù)
上兩種情況,由以上情況列出相應(yīng)關(guān)系式求實數(shù)
(2)當(dāng)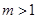 時,
時,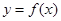 在
在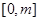 上是分段函數(shù),分段函數(shù)的最值,應(yīng)先求出函數(shù)在各部分的最值,然后取各部分的最值的最大值為整個函數(shù)的最大值.
上是分段函數(shù),分段函數(shù)的最值,應(yīng)先求出函數(shù)在各部分的最值,然后取各部分的最值的最大值為整個函數(shù)的最大值.
試題解析:
(1)方程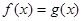 在
在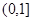 上有且僅一個實根
上有且僅一個實根
即方程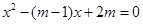 在
在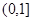 上有且僅一個實根 2分
上有且僅一個實根 2分
Ⅰ當(dāng)方程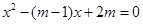 在
在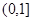 上有兩個相等實根
上有兩個相等實根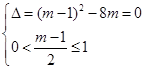 此時
此時 無解; 4分
無解; 4分
Ⅱ當(dāng)方程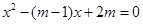 一根在
一根在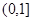 上一根不在
上一根不在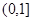 上分兩類情況
上分兩類情況
①在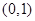 上有且僅一個實根,則
上有且僅一個實根,則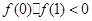
即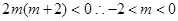 6分
6分
②當(dāng)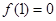 時,
時,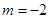 此時方程
此時方程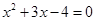
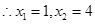 符合題意
符合題意
綜上所述,實數(shù) 的取值范圍
的取值范圍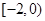 8分
8分
(2)Ⅰ當(dāng)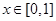 時,
時,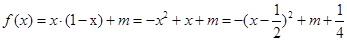
∴當(dāng)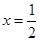 時,
時,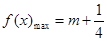 10分
10分
Ⅱ當(dāng)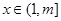 時,
時,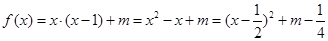
∵函數(shù)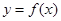 在
在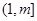 上單調(diào)遞增
上單調(diào)遞增
∴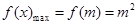 12分
12分
由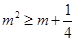 得
得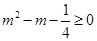 又
又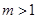

∴當(dāng)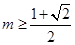 時,
時,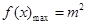 ,當(dāng)
,當(dāng)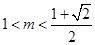 時,
時,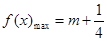 . 14分
. 14分
考點:二次方程的實根分布,分段函數(shù)求最值.


科目:高中數(shù)學(xué) 來源: 題型:解答題
一種放射性元素,最初的質(zhì)量為 ,按每年
,按每年 衰減.
衰減.
(1)求 年后,這種放射性元素的質(zhì)量
年后,這種放射性元素的質(zhì)量 與
與 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求這種放射性元素的半衰期(質(zhì)量變?yōu)樵瓉淼?img src="http://thumb.zyjl.cn/pic5/tikupic/99/3/t3b2c1.png" style="vertical-align:middle;" />時所經(jīng)歷的時間).( )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)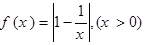
(1)當(dāng)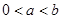 ,且
,且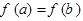 時,求證:
時,求證: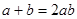
(2)是否存在實數(shù)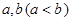 ,使得函數(shù)
,使得函數(shù)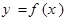 的定義域、值域都是
的定義域、值域都是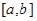 ?若存在,則求出
?若存在,則求出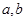 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) =
= ,
, =
= ,若曲線
,若曲線 和曲線
和曲線 都過點P(0,2),且在點P處有相同的切線
都過點P(0,2),且在點P處有相同的切線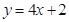 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若 時,
時, ≤
≤ ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) 的定義域為
的定義域為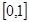 ,且同時滿足以下三個條件:①
,且同時滿足以下三個條件:①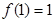 ;②對任意的
;②對任意的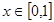 ,都有
,都有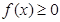 ;③當(dāng)
;③當(dāng)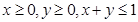 時總有
時總有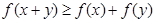 .
.
(1)試求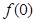 的值;
的值;
(2)求 的最大值;
的最大值;
(3)證明:當(dāng)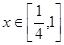 時,恒有
時,恒有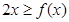 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
新晨投資公司擬投資開發(fā)某項新產(chǎn)品,市場評估能獲得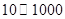 萬元的投資收益.現(xiàn)公司準(zhǔn)備制定一個對科研課題組的獎勵方案:獎金
萬元的投資收益.現(xiàn)公司準(zhǔn)備制定一個對科研課題組的獎勵方案:獎金 (單位:萬元)隨投資收益
(單位:萬元)隨投資收益 (單位:萬元)的增加而增加,且獎金不低于
(單位:萬元)的增加而增加,且獎金不低于 萬元,同時不超過投資收益的
萬元,同時不超過投資收益的 .
.
(1)設(shè)獎勵方案的函數(shù)模型為 ,試用數(shù)學(xué)語言表述公司對獎勵方案的函數(shù)模型
,試用數(shù)學(xué)語言表述公司對獎勵方案的函數(shù)模型 的基本要求.
的基本要求.
(2)下面是公司預(yù)設(shè)的兩個獎勵方案的函數(shù)模型:
① ; ②
; ②
試分別分析這兩個函數(shù)模型是否符合公司要求.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關(guān)系: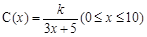 ,若不建隔熱層,每年能源消耗費用為8萬元.設(shè)
,若不建隔熱層,每年能源消耗費用為8萬元.設(shè) 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求k的值及 的表達(dá)式;
的表達(dá)式;
(2)隔熱層修建多厚時,總費用 達(dá)到最小,并求最小值.
達(dá)到最小,并求最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com