
已知函數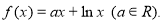
(1)若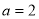 ,求曲線
,求曲線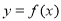 在
在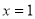 處的切線方程;
處的切線方程;
(2)求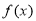 的單調區間;
的單調區間;
(3)設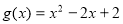 ,若對任意
,若對任意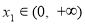 ,均存在
,均存在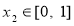 ,使得
,使得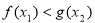 ,求
,求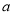 的取值范圍.
的取值范圍.
(1)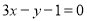 (2)詳見解析(3)
(2)詳見解析(3)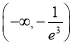
【解析】
試題分析:
(1)已知函數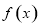 的解析式,把切點的橫坐標帶入函數
的解析式,把切點的橫坐標帶入函數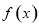 即可求出切點的縱坐標,對
即可求出切點的縱坐標,對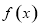 求導得到函數
求導得到函數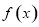 的導函數
的導函數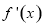 ,把
,把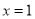 帶入導函數
帶入導函數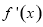 即可求的切線的斜率,利用點斜式即可得到切線的方程.
即可求的切線的斜率,利用點斜式即可得到切線的方程.
(2)對函數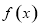 進行求導和求定義域,導函數
進行求導和求定義域,導函數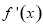 喊參數
喊參數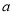 ,把
,把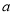 分為兩種情況進行討論,首先
分為兩種情況進行討論,首先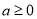 時,結合
時,結合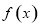 的定義域
的定義域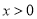 即可得到導函數在定義域內恒大于0,進而得到原函數在定義域內單調遞增,當
即可得到導函數在定義域內恒大于0,進而得到原函數在定義域內單調遞增,當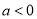 時,求解導函數
時,求解導函數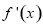 大于0和小于0的解集,得到原函數的單調遞增和單調遞減區間.
大于0和小于0的解集,得到原函數的單調遞增和單調遞減區間.
(3)該問題為存在性問題與恒成立問題的結合,即要求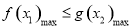 ,而
,而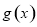 的最大值可以利用二次函數
的最大值可以利用二次函數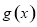 的圖像得到函數
的圖像得到函數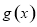 在區間
在區間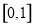 上的最值,函數
上的最值,函數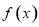 的最大值可以利用第二問的單調性求的,當
的最大值可以利用第二問的單調性求的,當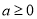 時,函數
時,函數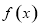 單調遞增,無最大值,故不符合題意,當
單調遞增,無最大值,故不符合題意,當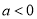 時,函數
時,函數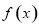 在
在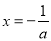 處前的最大值,帶入不等式即可求的
處前的最大值,帶入不等式即可求的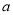 的取值范圍.
的取值范圍.
試題解析:
(1)由已知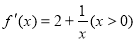 , 1分
, 1分
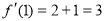 ,所以斜率
,所以斜率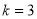 , 2分
, 2分
又切點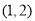 ,所以切線方程為
,所以切線方程為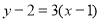 ),即
),即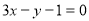
故曲線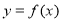 在
在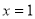 處切線的切線方程為
處切線的切線方程為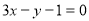 。 3分
。 3分
(2)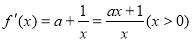 4分
4分
①當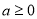 時,由于
時,由于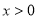 ,故
,故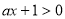 ,
,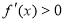 ,所以
,所以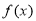 的單調遞增區間為
的單調遞增區間為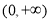 .
.
5分
②當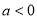 時,由
時,由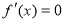 ,得
,得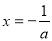 . 6分
. 6分
在區間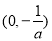 上,
上,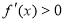 ,在區間
,在區間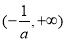 上,
上,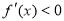 ,
,
所以,函數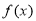 的單調遞增區間為
的單調遞增區間為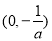 ,單調遞減區間為
,單調遞減區間為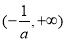 . 7分
. 7分
(3)由已知,轉化為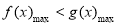 . 8分
. 8分
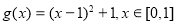 ,所以
,所以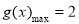 9分
9分
由(2)知,當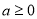 時,
時,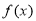 在
在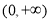 上單調遞增,值域為
上單調遞增,值域為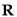 ,故不符合題意.
,故不符合題意.
(或者舉出反例:存在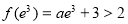 ,故不符合題意.) 10分
,故不符合題意.) 10分
當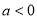 時,
時,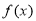 在
在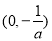 上單調遞增,在
上單調遞增,在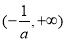 上單調遞減,
上單調遞減,
故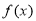 的極大值即為最大值,
的極大值即為最大值,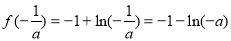 , 12分
, 12分
所以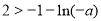 ,解得
,解得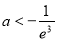 . 14分
. 14分
考點:恒成立問題存在性問題導數切線


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源:2013-2014學年廣東省揭陽市高三3月第一次模擬考試理科數學試卷(解析版) 題型:選擇題
定義一個集合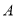 的所有子集組成的集合叫做集合
的所有子集組成的集合叫做集合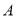 的冪集,記為
的冪集,記為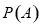 ,用
,用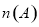 表示有限集
表示有限集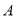 的元素個數,給出下列命題:①對于任意集合
的元素個數,給出下列命題:①對于任意集合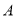 ,都有
,都有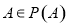 ;②存在集合
;②存在集合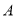 ,使得
,使得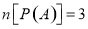 ;
;
③用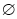 表示空集,若
表示空集,若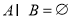 ,則
,則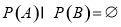 ;④若
;④若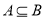 ,則
,則 ;⑤若
;⑤若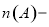
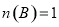 ,則
,則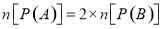 其中正確的命題個數為( )
其中正確的命題個數為( )
A.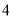 B.
B.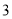 C.
C.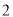 D.
D.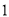
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省揭陽市高三3月第一次模擬考試文科數學試卷(解析版) 題型:填空題
根據某固定測速點測得的某時段內過往的 輛機動車的行駛速度(單位:
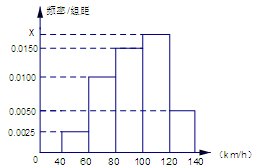
輛機動車的行駛速度(單位: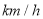 )繪制的頻率分布直方圖如圖所示.該路段限速標志牌提示機動車輛正常行駛速度為
)繪制的頻率分布直方圖如圖所示.該路段限速標志牌提示機動車輛正常行駛速度為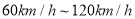 ,則該時段內過往的這
,則該時段內過往的這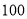 輛機動車中屬非正常行駛的有輛,圖中的
輛機動車中屬非正常行駛的有輛,圖中的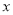 值為.
值為.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省揭陽市高三3月第一次模擬考試文科數學試卷(解析版) 題型:選擇題
如圖所示的程序框圖,能使輸入的 值與輸出的
值與輸出的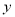 值相等的
值相等的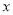 值分別為( )
值分別為( )
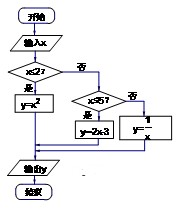
A.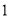 、
、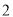 、
、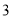 B.
B.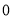 、
、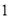 C.
C.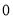 、
、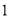 、
、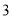 D.
D.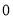 、
、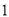 、
、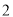 、
、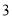 、
、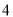
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省廣州市畢業班綜合測試二理科數學試卷(解析版) 題型:填空題
已知 表示不超過
表示不超過 的最大整數,例如
的最大整數,例如 ,
, .設函數
.設函數 ,當
,當 時,函數
時,函數 的值域為集合
的值域為集合 ,則
,則 中的元素個數為.
中的元素個數為.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三第二次模擬考試理科數學試卷(解析版) 題型:填空題
(坐標系與參數方程選做題)在極坐標系中,直線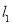 的方程是
的方程是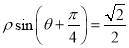 ,以極點為原
,以極點為原
點,以極軸為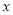 軸的正半軸建立直角坐標系,在直角坐標系中,直線
軸的正半軸建立直角坐標系,在直角坐標系中,直線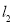 的方程是
的方程是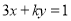 .如果直線
.如果直線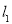 與
與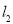
垂直,則常數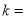 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com