Question

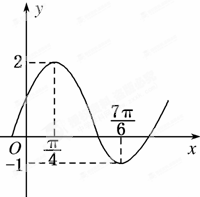
4．將函數f（x）=Asin（ωx+φ）+k（A＞0，ω＞0，0＜φ＜π）的圖象向右平移$\frac{2π}{3}$個單位，所得曲線的一部分如圖所示，則f（x）的解析式為（　　）

• A． f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x-$\frac{21π}{22}$）+1
• B． f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{21π}{22}$）+$\frac{1}{2}$
• C． f（x）=2sin（$\frac{11}{12}$x+$\frac{21π}{22}$）-$\frac{1}{2}$
• D． f（x）=$\frac{3}{2}$sin（$\frac{12}{11}$x+$\frac{5π}{22}$）+$\frac{1}{2}$

Answer 1

分析 由函數圖象求出f（x$-\frac{2π}{3}$）的解析式，然后結合函數的圖象平移求得f（x）的解析式．

解答 解：由圖可知，$\left\{\begin{array}{l}{A+k=2}\\{-A+k=-1}\end{array}\right.$，得A=$\frac{3}{2}$，k=$\frac{1}{2}$，
$\frac{T}{2}=\frac{7π}{6}-\frac{π}{4}$=$\frac{11π}{12}$，∴T=$\frac{11π}{6}$，
則$ω=\frac{2π}{T}=\frac{2π}{\frac{11π}{6}}=\frac{12}{11}$，
由$\frac{12}{11}×\frac{π}{4}+φ=\frac{π}{2}$，得φ=$\frac{5π}{22}$．
∴平移后的函數解析式為f（x$-\frac{2π}{3}$）=$\frac{3}{2}sin（\frac{12}{11}x$$+\frac{5π}{22}）$$+\frac{1}{2}$．
∴f（x）=$\frac{3}{2}sin[\frac{12}{11}（x+\frac{2π}{3}）+\frac{5π}{22}]+\frac{1}{2}$=$\frac{3}{2}sin（\frac{12}{11}x+\frac{21π}{22}）+\frac{1}{2}$．
故選：B．

點評 本題考查由y=Asin（ωx+φ）的部分圖象求函數解析式，利用五點作圖的某一點求φ是關鍵，是中檔題．