
【題目】已知函數f(x)=2x- ![]() 的定義域為(0,1](a為實數).
的定義域為(0,1](a為實數).
(1)當a=1時,求函數y=f(x)的值域;
(2)求函數y=f(x)在區間(0,1]上的最大值及最小值,并求出當函數f(x)取得最值時x的值.
【答案】
(1)解:當a=1時,f(x)=2x- ![]() ,任取1≥x1>x2>0,
,任取1≥x1>x2>0,
則f(x1)-f(x2)=2(x1-x2)- ![]() =(x1-x2)
=(x1-x2) ![]() .
.
∵1≥x1>x2>0,∴x1-x2>0,x1x2>0.
∴f(x1)>f(x2),∴f(x)在(0,1]上單調遞增,無最小值,當x=1時取得最大值1,所以f(x)的值域為(-∞,1].
(2)解:當a≥0時,y=f(x)在(0,1]上單調遞增,無最小值,當x=1時取得最大值2-a;
當a<0時,f(x)=2x+ ![]() ,
,
當 ![]() ≥1,即a∈(-∞,-2]時,y=f(x)在(0,1]上單調遞減,無最大值,當x=1時取得最小值2-a;
≥1,即a∈(-∞,-2]時,y=f(x)在(0,1]上單調遞減,無最大值,當x=1時取得最小值2-a;
當 ![]() <1,即a∈(-2,0)時,y=f(x)在
<1,即a∈(-2,0)時,y=f(x)在 ![]() 上單調遞減,在
上單調遞減,在 ![]()
上單調遞增,無最大值,當x= ![]() 時取得最小值2
時取得最小值2 ![]() .
.
【解析】本題主要考查求解函數的值域以及最值問題。(1)利用函數的單調性求函數的值域問題。(2)根據函數的單調性求函數在區間上的最值問題。


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:
【題目】心理學家分析發現視覺和空間能力與性別有關,某數學興趣小組為了驗證這個結論,從興趣小組中按分層抽樣的方法抽取 ![]() 名同學(男
名同學(男 ![]() 人,女
人,女 ![]() 人),給所有同學幾何題和代數題各一題,讓各位同學只能自由選擇其中一道題進行解答.選題情況如下表(單位:人):
人),給所有同學幾何題和代數題各一題,讓各位同學只能自由選擇其中一道題進行解答.選題情況如下表(單位:人):
幾何題 | 代數題 | 總計 | |
男同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
幾何題 | 代數題 | 總計 | |
男同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
附表及公式: ![]()

(1)能否據此判斷有 ![]() 的把握認為視覺和空間能力與性別有關?
的把握認為視覺和空間能力與性別有關?
(2)現從選擇做幾何題的 ![]() 名女生中,任意抽取兩人,對她們的答題情況進行全程研究,記甲、乙兩位女生被抽到的人數為
名女生中,任意抽取兩人,對她們的答題情況進行全程研究,記甲、乙兩位女生被抽到的人數為 ![]() ,求
,求 ![]() 的分布列和
的分布列和 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代名著《莊子天下篇》中有一句名言“一尺之棰,日取其半,萬世不竭”,其意思為:一尺的木棍,每天截取一半,永遠都截不完,現將該木棍依此規律截取,如圖所示的程序框圖的功能就是計算截取7天后所剩木棍的長度(單位:尺),則①②③處可分別填入的是( )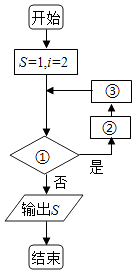
A.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
B.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
C.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
D.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com