
分析 令t=($\frac{1}{3}$)x,則y=f(x)=1+at+t2,
(1)當a=-2,x∈[1,2]時,y=f(x)=1-2t+t2,t∈[$\frac{1}{9}$,$\frac{1}{3}$],結合二次函數的圖象和性質,可得函數f(x)的最大值與最小值;
(2)若函數f(x)在[1,+∞)上都有-2≤f(x)≤3,y=1+at+t2,在(0,$\frac{1}{3}$]上都有-2≤y≤3,結合二次函數的圖象和性質,可得實數a的取值范圍.
解答 解:令t=($\frac{1}{3}$)x,則y=f(x)=1+at+t2,
(1)當a=-2,x∈[1,2]時,y=f(x)=1-2t+t2,t∈[$\frac{1}{9}$,$\frac{1}{3}$],
當t=$\frac{1}{9}$,即x=2時,函數f(x)的最大值為$\frac{64}{81}$,
當t=$\frac{1}{3}$,即x=1時,函數f(x)的最小值為$\frac{4}{9}$,
(2)若函數f(x)在[1,+∞)上都有-2≤f(x)≤3,
則y=1+at+t2,在(0,$\frac{1}{3}$]上都有-2≤y≤3,
由函數y=1+at+t2的圖象是開口朝上,且以直線t=$-\frac{a}{2}$為對稱軸的直線,
故當$-\frac{a}{2}$≤0,即a≥0時,1+$\frac{1}{3}$a+$\frac{1}{9}$≤3,解得:a∈[0,$\frac{17}{3}$]
當0<$-\frac{a}{2}$<$\frac{1}{3}$,即$-\frac{2}{3}$<a<0時,$\left\{\begin{array}{l}\frac{4-{a}^{2}}{4}≥-2\\ 1+\frac{1}{3}a+\frac{1}{9}≤3\end{array}\right.$,解得:a∈($-\frac{2}{3}$,0),
當$-\frac{a}{2}$≥$\frac{1}{3}$,即a≤$-\frac{2}{3}$時,1+$\frac{1}{3}$a+$\frac{1}{9}$≥-2,解得:a∈[-$\frac{28}{3}$,$-\frac{2}{3}$]
綜相可得a∈[-$\frac{28}{3}$,$\frac{17}{3}$].
點評 本題考查的知識點是函數的最值,恒成立問題,二次函數的圖象和性質,分類討論思想,難度中檔.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-3,-1) | B. | [-3,2) | C. | (-∞,-3]∪(2,+∞) | D. | (-∞,-3]∪(-1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
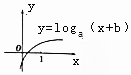 已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )
已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )| A. | $\frac{1}{b^4}$ | B. | $\frac{1}{b^5}$ | C. | b4 | D. | b5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com