
【題目】已知A、B是函數y=f(x),x∈[a,b]圖象的兩個端點,M(x,y)是f(x)上任意一點,過M(x,y)作MN⊥x軸交直線AB于N,若不等式|MN|≤k恒成立,則稱函數f(x)在[a,b]上“k階線性近似”.
(1)若f(x)=x+ ![]() ,x∈[
,x∈[ ![]() ,2],證明:f(x)在[
,2],證明:f(x)在[ ![]() ,2]上“
,2]上“ ![]() 階線性近似”;
階線性近似”;
(2)若f(x)=x2在[﹣1,2]上“k階線性近似”,求實數k的最小值.
【答案】
(1)證明:若f(x)=x+ ![]() ,x∈[
,x∈[ ![]() ,2],則A(
,2],則A( ![]() ,
, ![]() )、B(2,
)、B(2, ![]() ),
),
故直線AB的方程為:y= ![]() ,
,
則由|MN|= ![]() ﹣(x+
﹣(x+ ![]() ),
),
∴|MN|∈[0, ![]() ],
],
故|MN|≤ ![]() ,
,
故f(x)在[ ![]() ,2]上“
,2]上“ ![]() 階線性近似”
階線性近似”
(2)解:由MN⊥x交直線AB于N,得 N 和M的橫坐標相同.
對于區間[﹣1,2]上的函數f(x)=x2 ,A(﹣1,1)、B(2,4),
則直線AB的方程為:y=x+2,
則有|MN|=x+2﹣x2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴|MN|∈[0, ![]() ].
].
再由|MN|≤k恒成立,可得 k≥ ![]() .
.
故實數k的最小值為 ![]() .
.
【解析】(1)根據對勾函數的圖象和性質,得到f(x)=x+ ![]() ,x∈[
,x∈[ ![]() ,2],滿足|MN|≤
,2],滿足|MN|≤ ![]() ,進而得到答案.(2)由已知可得 N和M的橫坐標相同,根據|MN|=x+2﹣x2=﹣(x﹣
,進而得到答案.(2)由已知可得 N和M的橫坐標相同,根據|MN|=x+2﹣x2=﹣(x﹣ ![]() )2+
)2+ ![]() 及x∈[﹣1,2],求出|MN|的范圍,再由|MN|≤k恒成立,求得k的取值范圍.
及x∈[﹣1,2],求出|MN|的范圍,再由|MN|≤k恒成立,求得k的取值范圍.
【考點精析】認真審題,首先需要了解函數的圖象(函數的圖像是由直角坐標系中的一系列點組成;圖像上每一點坐標(x,y)代表了函數的一對對應值,他的橫坐標x表示自變量的某個值,縱坐標y表示與它對應的函數值).


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數學 來源: 題型:
【題目】設不等式組 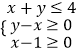 ,表示的平面區域為D,若圓C:(x+1)2+(y+1)2=r2(r>0)經過區域D上的點,則r的取值范圍是( )
,表示的平面區域為D,若圓C:(x+1)2+(y+1)2=r2(r>0)經過區域D上的點,則r的取值范圍是( )
A.[2 ![]() ,2
,2 ![]() ]
]
B.(2 ![]() ,3
,3 ![]() ]??
]??
C.(3 ![]() ,2
,2 ![]() ]
]
D.(0,2 ![]() )∪(2
)∪(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分組的頻率分布直方圖如圖. 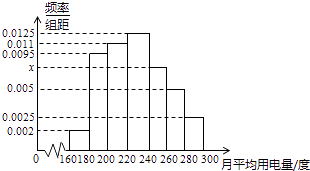
(1)求直方圖中x的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為,[220,240),[240,260),[260,280),[280,300)的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在[220,240)的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將直線2x﹣y+λ=0沿x軸向左平移1個單位,所得直線與圓x2+y2+2x﹣4y=0相切,則實數λ的值為( )
A.﹣3或7
B.﹣2或8
C.0或10
D.1或11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線x2=4y,圓C:x2+(y﹣2)2=4,點M(x0 , y0),(x0>0,y0>4)為拋物線上的動點,過點M的圓C的兩切線,設其斜率分別為k1 , k2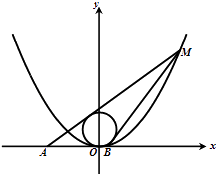
(Ⅰ)求證:k1+k2= ![]() ,k1k2=
,k1k2= ![]() .
.
(Ⅱ)求過點M的圓的兩切線與x軸圍成的三角形面積S的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在等腰梯形CDEF中,DE=CD= ![]() ,EF=2+
,EF=2+ ![]() ,將它沿著兩條高AD,CB折疊成如圖(2)所示的四棱錐E﹣ABCD(E,F重合).
,將它沿著兩條高AD,CB折疊成如圖(2)所示的四棱錐E﹣ABCD(E,F重合). 
(1)求證:BE⊥DE;
(2)設點M為線段AB的中點,試在線段CE上確定一點N,使得MN∥平面DAE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com