【題目】設不等式組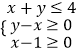 
，表示的平面區域為D，若圓C：（x+1）2+（y+1）2=r2（r＞0）經過區域D上的點，則r的取值范圍是（ ）
A.[2 
，2 
]
B.（2 ，3 ]??
C.（3 ，2 ]
D.（0，2 ）∪（2 ，+∞）
天天練口算系列答案科目：高中數學 來源： 題型：
【題目】如圖，在直角梯形ABCD中，AD∥BC，∠BAD= 
，AB=BC=1，AD=2，E是AD的中點，O是AC與BE的交點，將ABE沿BE折起到A1BE的位置，如圖2． （Ⅰ）證明：CD⊥平面A1OC；
（Ⅱ）若平面A1BE⊥平面BCDE，求平面A1BC與平面A1CD夾角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設某等腰三角形的底角為α，頂角為β，且cosβ= 
． （Ⅰ）求sinα的值；
（Ⅱ）若函數f（x）=tanx在[﹣ 
，α]上的值域與函數g（x）=2sin（2x﹣ ）在[0，m]上的值域相同，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a為實數，p：點M（1，1）在圓（x+a）2+（y﹣a）2=4的內部； q：x∈R，都有x2+ax+1≥0．
（1）若p為真命題，求a的取值范圍；
（2）若q為假命題，求a的取值范圍；
（3）若“p且q”為假命題，且“p或q”為真命題，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知A、B是函數y=f（x），x∈[a，b]圖象的兩個端點，M（x，y）是f（x）上任意一點，過M（x，y）作MN⊥x軸交直線AB于N，若不等式|MN|≤k恒成立，則稱函數f（x）在[a，b]上“k階線性近似”．
（1）若f（x）=x+ 
，x∈[ 
，2]，證明：f（x）在[ ，2]上“ 階線性近似”；
（2）若f（x）=x2在[﹣1，2]上“k階線性近似”，求實數k的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐V﹣ABC中，平面VAB⊥平面ABC，△VAB為等邊三角形，AC⊥BC且AC=BC= 
，O，M分別為AB，VA的中點． 
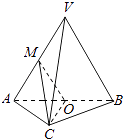
（1）求證：VB∥平面MOC；
（2）求證：平面MOC⊥平面VAB
（3）求三棱錐V﹣ABC的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2+y2﹣2x﹣4y+1=0．
（1）求過點M（3，1）的圓C的切線方程；
（2）若直線l：ax﹣y+4=0與圓C相交于A，B兩點，且弦AB的長為 
，求a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
