
分析 (1)求出函數的定義域,函數的導數,判斷函數的單調性,利用函數的零點個數,推出結果.
(2)x1,x2是f(x)的兩個零點,通過lnx1-x1=lna,lnx2-x2=lna,則$a=\frac{x_1}{{{e^{x_1}}}},a=\frac{x_2}{{{e^{x_2}}}}$,
設$g(x)=\frac{x}{e^x}$,$g'(x)=\frac{1-x}{e^x}$,利用g(x)在(0,1)上遞增,在(1,+∞)上遞減,利用函數g(x)圖象與直線y=a都有兩個交點.橫坐標分別為x1,x2,且x1∈(0,1),x2∈(1,+∞),結合函數的圖象,利用函數的單調性以及存在性,推出結論.
解答 解:(1)f(x)的定義域為(0,+∞).$f'(x)=\frac{1-x}{x}$,
由f'(x)>0得:0<x<1;由f'(x)<0得:x>1.
故f(x)在(0,1)上遞增,在(1,+∞)上遞減.
要使f(x)有兩個零點,則f(1)>0,解得:$0<a<\frac{1}{e}$.…(5分)
(2)∵x1,x2是f(x)的兩個零點,∴lnx1-x1=lna,lnx2-x2=lna,則$a=\frac{x_1}{{{e^{x_1}}}},a=\frac{x_2}{{{e^{x_2}}}}$,.
設$g(x)=\frac{x}{e^x}$,$g'(x)=\frac{1-x}{e^x}$,所以g(x)在(0,1)上遞增,在(1,+∞)上遞減,故對任意$a∈(0,\frac{1}{e})$,函數g(x)圖象與直線y=a都有兩個交點.橫坐標分別為x1,x2,且x1∈(0,1),x2∈(1,+∞),如下圖: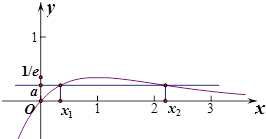
…(9分)
任取${a_1},{a_2}∈(0,\frac{1}{e})$,設a1<a2,則有g(ξ1)=g(ξ2)=a1,0<ξ1<1<ξ2,g(η1)=g(η2)=a2,0<η1<1<η2,由a1<a2得:g(ξ1)<g(η1),∵g(x)在(0,1)上遞增,∴ξ1<η1,同理得:ξ2>η2,所以$\frac{ξ_1}{ξ_2}<\frac{η_1}{η_2}$,
故$\frac{x_1}{x_2}$的值隨a的值增大而增大.…(12分)
點評 本題考查函數的導數的綜合應用,構造法以及函數的圖象的應用,考查轉化思想以及計算能力.難度比較大.


科目:高中數學 來源: 題型:選擇題
| A. | [0,2] | B. | [1,2] | C. | [-2,0] | D. | [-2,-1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
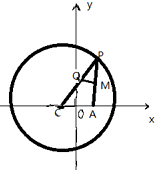 已知點C為圓(x+1)2+y2=8的圓心,P是圓上的動點,點Q在圓的半徑CP上,且有點A(1,0)和AP上的點M,滿足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知點C為圓(x+1)2+y2=8的圓心,P是圓上的動點,點Q在圓的半徑CP上,且有點A(1,0)和AP上的點M,滿足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
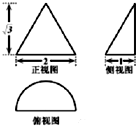
| A. | $\frac{\sqrt{3}π}{2}$ | B. | $\frac{\sqrt{3}π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{\sqrt{3}π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4032π}$ | B. | $\frac{1}{2016π}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{2016}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com