
【題目】哈師大附中高三學年統計甲、乙兩個班級一模數學分數(滿分150分),每個班級20名同學,現有甲、乙兩位同學的20次成績如下列莖葉圖所示:
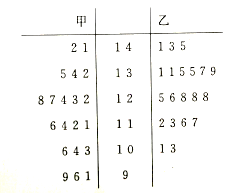
(I)根據基葉圖求甲、乙兩位同學成績的中位數,并將乙同學的成績的頻率分布直方圖填充完整;
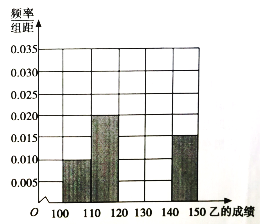
(Ⅱ)根據基葉圖比較甲乙兩位同學數學成績的平均值及穩定程度(不要求計算出具體值,給出結論即可)
(Ⅲ)現從甲乙兩位同學的不低于140分的成績中任意選出2個成績,設事件![]() 為“其中2 個成績分別屬于不同的同學”,求事件
為“其中2 個成績分別屬于不同的同學”,求事件![]() 發生的概率.
發生的概率.
【答案】(I)見解析.
(Ⅱ)乙的成績的平均分比甲的成績的平均分高,乙同學的成績比甲同學的成績更穩定集中.
(III)![]() .
.
【解析】分析:(I)根據中位數的定義可得甲、乙兩位同學成績的中位數,由莖葉圖可得頻數,由頻數得頻率,從而可得縱坐標,進而可補全直方圖;(Ⅱ)從莖葉圖可以看出,乙的成績的平均分比甲的成績的平均分高,乙同學的成績比甲同學的成績更穩定集中;(III)利用列舉法,甲乙兩位同學的不低于140分的成績中任意選出2個成績的基本事件有![]() 個,其中2個成績分屬不同同學的事件有
個,其中2個成績分屬不同同學的事件有![]() 個,利用古典概型概率公式可得結果.
個,利用古典概型概率公式可得結果.
詳解:(I)甲的成績的中位數是119,乙的成績的中位數是128,
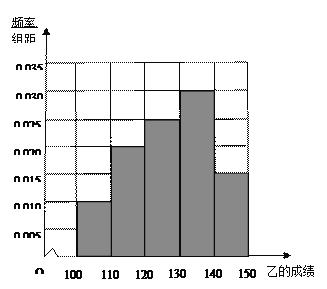
(II)
從莖葉圖可以看出,乙的成績的平均分比甲的成績的平均分高,乙同學的成績比甲同學的成績更穩定集中 . (III)甲同學的不低于140分的成績有2個設為a,b,乙同學的不低于140分的成績有3個,設為c,d,e
現從甲乙兩位同學的不低于140分的成績中任意選出2個成績有:(a,b),(a,c)(a,d)(a,e)(b,c)(b,d)(b,e)(c,d)(c,e)(d,e)共10種,
其中2個成績分屬不同同學的情況有: (a,c)(a,d)(a,e)(b,c)(b,d)(b,e)共6種
因此事件A發生的概率P(A)=![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】為了解中學生對交通安全知識的掌握情況,從農村中學和城鎮中學各選取100名同學進行交通安全知識競賽.下圖1和圖2分別是對農村中學和城鎮中學參加競賽的學生成績按![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.
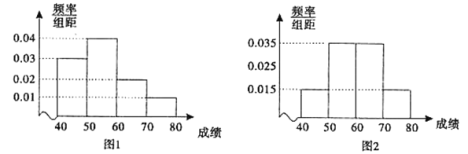
(Ⅰ)分別估算參加這次知識競賽的農村中學和城鎮中學的平均成績;
(Ⅱ)完成下面![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
成績小于60分人數 | 成績不小于60分人數 | 合計 | |
農村中學 | |||
城鎮中學 | |||
合計 |
附:![]()
臨界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:橢圓![]() 的頂點為
的頂點為![]() ,左右焦點分別為
,左右焦點分別為![]() ,
,![]() ,
,![]()
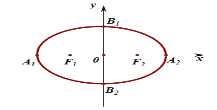
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究在
兩點,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?若存在求出點
為定值?若存在求出點![]() 的坐標,若不存在請說明理由?
的坐標,若不存在請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以原點為極點,以![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(1)若曲線![]() 參數方程為:
參數方程為:![]() (
(![]() 為參數),求曲線
為參數),求曲線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)若曲線![]() 參數方程為:
參數方程為:![]() (
(![]() 為參數),
為參數),![]() ,且曲線
,且曲線![]() 與曲線
與曲線![]() 交點分別為
交點分別為![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視廠家準備在五一舉行促銷活動,現在根據近七年的廣告費與銷售量的數據確定此次廣告費支出.廣告費支出x(萬元)和銷售量y(萬臺)的數據如下:

(1)若用線性回歸模型擬合y與x的關系,求出y關于x的線性回歸方程(其中![]() ;參考方程:回歸直線
;參考方程:回歸直線 ,
,![]() )
)
(2)若用模型![]() 擬合y與x的關系,可得回歸方程
擬合y與x的關系,可得回歸方程![]() ,經計算線性回歸模型和該模型的
,經計算線性回歸模型和該模型的![]() 分別約為0.75和0.88,請用
分別約為0.75和0.88,請用![]() 說明選擇哪個回歸模型更好;
說明選擇哪個回歸模型更好;
(3)已知利潤z與x,y的關系為z=200y﹣x.根據(2)的結果回答:當廣告費x=20時,銷售量及利潤的預報值是多少?(精確到0.01)參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,焦距為
,焦距為![]() ,點
,點![]() 為橢圓上一點,
為橢圓上一點,![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求橢圓的標準方程;
(2)設點![]() 為橢圓的上頂點,過橢圓內一點
為橢圓的上頂點,過橢圓內一點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點,若
兩點,若![]() 與
與![]() 的面積比為
的面積比為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() ,現在沿
,現在沿![]() 將
將![]() 折起使點
折起使點![]() 到點P處,得到三棱錐
到點P處,得到三棱錐![]() ,且平面
,且平面![]() 平面
平面![]() .
.


(1)棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?請說明你的結論;
?請說明你的結論;
(2)求證:![]() 平面
平面![]() ;
;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,A,B,C三點滿足![]() 。
。
(1)求證:A,B,C三點共線;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0, ![]() ],函數f(x)=
],函數f(x)=![]() (2m+
(2m+![]() )|
)|![]() |+m2的最小值為5,求實數m的值。
|+m2的最小值為5,求實數m的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com