
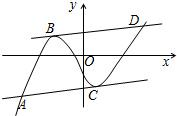
 三次函數f(x)=x3+ax2+bx+c的圖象如圖所示,直線BD∥AC,且直線BD與函數圖象切于點B,交于點D,直線AC與函數圖象切于點C,交于點A.
三次函數f(x)=x3+ax2+bx+c的圖象如圖所示,直線BD∥AC,且直線BD與函數圖象切于點B,交于點D,直線AC與函數圖象切于點C,交于點A.| 2a |
| 3 |
|
|
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
| 2a |
| 3 |
| 2a |
| 3 |


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖南師大附中高三第一次月考數學試卷(理科)(解析版) 題型:填空題
 ,請你根據上面探究結果,解答以下問題
,請你根據上面探究結果,解答以下問題 x3-
x3- x2+3x-
x2+3x-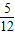 的對稱中心為 ;
的對稱中心為 ; +…+f(
+…+f(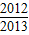 )= .
)= .查看答案和解析>>
科目:高中數學 來源:2012-2013學年四川省成都市雙流縣棠湖中學高三(上)11月月考數學試卷(文科)(解析版) 題型:填空題
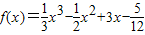 ,請你根據上面探究結果,解答以下問題
,請你根據上面探究結果,解答以下問題 x3-
x3- x2+3x-
x2+3x-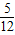 的對稱中心為 ;
的對稱中心為 ;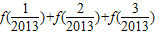 +…+f(
+…+f(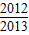 )= .
)= .查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省湛江師范附中高考復習數學模擬試卷3(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com