
【題目】如果函數(shù)![]() 在其定義域內存在實數(shù)
在其定義域內存在實數(shù)![]() ,使得
,使得![]() 成立,則稱函數(shù)
成立,則稱函數(shù)![]() 為“可拆分函數(shù)”.
為“可拆分函數(shù)”.
(1)試判斷函數(shù)![]() 是否為“可拆分函數(shù)”?并說明你的理由;
是否為“可拆分函數(shù)”?并說明你的理由;
(2)證明:函數(shù)![]() 為“可拆分函數(shù)”;
為“可拆分函數(shù)”;
(3)設函數(shù)![]() 為“可拆分函數(shù)”,求實數(shù)
為“可拆分函數(shù)”,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) 不是“可分拆函數(shù)”(2)見解析(3)![]()
【解析】試題分析: (1)按照“可分拆函數(shù)”的概念,只需方程有根即可,據(jù)此判斷;
(2)本問利用零點定理即可判斷,即判斷端點處的函數(shù)值異號即可證明結論;
(3)若函數(shù)在(0,+∞)上為可分拆函數(shù),只需方程在該區(qū)間上有實根,然后借助于換元的方法,將![]() ,然后分離參數(shù)方法,即可求出
,然后分離參數(shù)方法,即可求出![]() 的取值范圍.
的取值范圍.
試題解析:
(1)假設![]() 是“可分拆函數(shù)”,則存在
是“可分拆函數(shù)”,則存在![]() ,使得
,使得![]()
即![]() ,而此方程的判別式
,而此方程的判別式![]() ,方程無實數(shù)解,
,方程無實數(shù)解,
所以,![]() 不是“可分拆函數(shù)”.
不是“可分拆函數(shù)”.
(2)令![]() ,
,
則![]() ,
,
又![]() 故
故![]() ,
,
所以![]() 在上有實數(shù)解
在上有實數(shù)解![]() ,也即存在實數(shù)
,也即存在實數(shù)![]() ,使得
,使得
![]() 成立,
成立,
所以![]() 是“可分拆函數(shù)”.
是“可分拆函數(shù)”.
(3)因為函數(shù)![]() 為“可分拆函數(shù)”,
為“可分拆函數(shù)”,
所以存在實數(shù)![]() ,使得
,使得![]() =
=![]() +
+![]() ,
,
![]() =
=![]() 且
且![]() ,所以
,所以![]() ,
,
![]() ,則
,則![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.


 優(yōu)學名師名題系列答案
優(yōu)學名師名題系列答案科目:高中數(shù)學 來源: 題型:
【題目】國家射擊隊的某隊員射擊一次,命中7~10環(huán)的概率如表所示:
命中環(huán)數(shù) | 10環(huán) | 9環(huán) | 8環(huán) | 7環(huán) |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該射擊隊員射擊一次 求:
(1)射中9環(huán)或10環(huán)的概率;
(2)至少命中8環(huán)的概率;(3)命中不足8環(huán)的概率。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的方程為x2+y2-8x+15=0,若直線y=kx-2上至少存在一點,使得以該點為圓心,1為半徑的圓與圓C有公共點,則k的取值范圍是( )
A.![]()
B.k<0或![]()
C.![]()
D.![]() 或
或![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】
如圖,四棱錐P -ABCD的底面是矩形,側面PAD是正三角形,
且側面PAD⊥底面ABCD,E 為側棱PD的中點。
(1)求證:PB//平面EAC;
(2)求證:AE⊥平面PCD;
(3)當![]() 為何值時,PB⊥AC ?
為何值時,PB⊥AC ?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將邊長為1的正方形AA1O1O(及其內部)繞OO1旋轉一周形成圓柱,如圖, 弧AC 長為 ![]() ,弧A1B1 長為
,弧A1B1 長為 ![]() ,其中B1與C在平面AA1O1O的同側.
,其中B1與C在平面AA1O1O的同側. 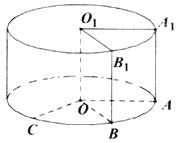
(1)求圓柱的體積與側面積;
(2)求異面直線O1B1與OC所成的角的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 的最大值為3,其圖象相鄰兩條對稱軸之間的距離為
的最大值為3,其圖象相鄰兩條對稱軸之間的距離為![]() .
.
(Ⅰ)求函數(shù)![]() 的解析式和當
的解析式和當![]() 時
時![]() 的單調減區(qū)間;
的單調減區(qū)間;
(Ⅱ)![]() 的圖象向右平行移動
的圖象向右平行移動![]() 個長度單位,再向下平移1個長度單位,得到
個長度單位,再向下平移1個長度單位,得到![]() 的圖象,用“五點法”作出
的圖象,用“五點法”作出![]() 在
在![]() 內的大致圖象.
內的大致圖象.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知 ![]() R,函數(shù)
R,函數(shù) ![]() =
= ![]() .
.
(1)當 ![]() 時,解不等式
時,解不等式 ![]() >1;
>1;
(2)若關于 ![]() 的方程
的方程 ![]() +
+ ![]() =0的解集中恰有一個元素,求
=0的解集中恰有一個元素,求 ![]() 的值;
的值;
(3)設 ![]() >0,若對任意
>0,若對任意 ![]()
![]() ,函數(shù)
,函數(shù) ![]() 在區(qū)間
在區(qū)間 ![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com