
【題目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(3,﹣
=(3,﹣ ![]() ),x∈[0,π].
),x∈[0,π].
(1)若 ![]() ∥
∥ ![]() ,求x的值;
,求x的值;
(2)記f(x)= ![]() ,求f(x)的最大值和最小值以及對應的x的值.
,求f(x)的最大值和最小值以及對應的x的值.
【答案】
(1)解:∵ ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(3,﹣
=(3,﹣ ![]() ),
), ![]() ∥
∥ ![]() ,
,
∴﹣ ![]() cosx=3sinx,
cosx=3sinx,
∴tanx=﹣ ![]() ,
,
∵x∈[0,π],
∴x= ![]() ,
,
(2)解:f(x)= ![]() =3cosx﹣
=3cosx﹣ ![]() sinx=2
sinx=2 ![]() (
( ![]() cosx﹣
cosx﹣ ![]() sinx)=2
sinx)=2 ![]() cos(x+
cos(x+ ![]() ),
),
∵x∈[0,π],
∴x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴﹣1≤cos(x+ ![]() )≤
)≤ ![]() ,
,
當x=0時,f(x)有最大值,最大值3,
當x= ![]() 時,f(x)有最小值,最小值﹣2
時,f(x)有最小值,最小值﹣2 ![]() .
.
【解析】(1)先由 ![]() //
//![]() 及同角三角函數的基本關系可得tanx,再利用x∈[0,π]可得x的值;(2)先由數量積的坐標公式和輔助角公式可得f(x)=2
及同角三角函數的基本關系可得tanx,再利用x∈[0,π]可得x的值;(2)先由數量積的坐標公式和輔助角公式可得f(x)=2 ![]() cos(x+
cos(x+ ![]() ),再由x的取值范圍]可得x+
),再由x的取值范圍]可得x+ ![]() 的取值范圍,進而可得cos(x+
的取值范圍,進而可得cos(x+ ![]() )的取值范圍,從而可得f(x)的最大值和最小值以及對應的x的值.
)的取值范圍,從而可得f(x)的最大值和最小值以及對應的x的值.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】設集合M={x|x<2},集合N={x|0<x<1},則下列關系中正確的是( )
A.M∪N=R
B.M∪RN=R
C.N∪RM=R
D.M∩N=M
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,邊a、b、c分別是角A、B、C的對邊,且滿足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面積為4![]() ,b=4
,b=4![]() ,求△ABC的周長
,求△ABC的周長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+ ![]() ,a∈R.
,a∈R.
(1)若f(x)的最小值為0,求實數a的值;
(2)證明:當a=2時,不等式f(x)≥ ![]() ﹣e1﹣x恒成立.
﹣e1﹣x恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點D,E,F.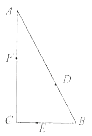
(1)若甲、乙都以每分鐘100m的速度從點B出發在各自的大道上奔走,到大道的另一端時即停,乙比甲遲2分鐘出發,當乙出發1分鐘后,求此時甲乙兩人之間的距離;
(2)設∠CEF=θ,乙丙之間的距離是甲乙之間距離的2倍,且∠DEF= ![]() ,請將甲乙之間的距離y表示為θ的函數,并求甲乙之間的最小距離.
,請將甲乙之間的距離y表示為θ的函數,并求甲乙之間的最小距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某服裝批發市場1-5月份的服裝銷售量![]() 與利潤
與利潤![]() 的統計數據如下表:
的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷售量 | 3 | 6 | 4 | 7 | 8 |
利潤 | 19 | 34 | 26 | 41 | 46 |
(1)從這五個月的利潤中任選2個,分別記為![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知銷售量![]() 與利潤
與利潤![]() 大致滿足線性相關關系,請根據前4個月的數據,求出
大致滿足線性相關關系,請根據前4個月的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的利潤的估計數據與真實數據的誤差不超過2萬元,則認為得到的利潤的估計數據是理想的.請用表格中第5個月的數據檢驗由(2)中回歸方程所得的第5個月的利潤的估計數據是否理想.參考公式:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+2a|+|x﹣1|,a∈R.
(1)當a=1時,解不等式f(x)≤5;
(2)若f(x)≥2對于x∈R恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:2a1+22a2+23a3+…+2nan=n(n∈N*),數列{ ![]() }的前n項和為Sn , 則S1S2S3…S10= .
}的前n項和為Sn , 則S1S2S3…S10= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com