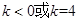由題意,當k>0時,函數定義域是(0,+∞),當k<0時,函數定義域是(-1,0)
當k>0時,lgkx=2lg(x+1)
∴lgkx-2lg(x+1)=0
∴lgkx-lg(x+1)2=0,即kx=(x+1)2在(0,+∞)僅有一個解
∴x2-(k-2)x+1=0在(0,+∞)僅有一個解
令f(x)=x2-(k-2)x+1
又當x=0時,f(x)=x2-(k-2)x+1=1>0
∴△=(k-2)2-4=0
∴k-2=±2
∴k=0舍,或4
k=0時lgkx無意義,舍去
∴k=4
當k<0時,函數定義域是(-1,0)
函數y=kx是一個遞減過(-1,-k)與(0,0)的線段,函數y=(x+1)2在(-1,0)遞增且過兩點(-1,0)與(0,1),此時兩曲線段恒有一個交點,故k<0符合題意
故答案為:k=4或k<0.

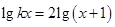 僅有一個實根,那么
僅有一個實根,那么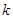 的取值范圍是 .
的取值范圍是 .