
【題目】中國男子籃球甲級聯(lián)賽的規(guī)則規(guī)定:每場比賽勝者得2 分, 負者得1 分(每場比賽, 即使通過加時賽也必須分出勝負).某男籃甲級隊實力強勁, 每場比賽獲勝的概率為![]() 、失利的概率為
、失利的概率為![]() .求該隊在賽程中間通過若干場比賽獲得n 分的概率(設(shè)該隊這一賽季的全部比賽場次數(shù)為S,這里0<n ≤S).
.求該隊在賽程中間通過若干場比賽獲得n 分的概率(設(shè)該隊這一賽季的全部比賽場次數(shù)為S,這里0<n ≤S).
【答案】見解析
【解析】
設(shè)經(jīng)過若干場比賽,該隊獲![]() 分的概率為
分的概率為![]() ,則由
,則由![]() .
.
當(dāng)![]() 時,有
時,有
![]() ,
,
![]() .
.
因此,數(shù)列![]() 是首項為
是首項為![]() 、公比為
、公比為![]() 的等比數(shù)列,有
的等比數(shù)列,有
![]() .
.
故![]()
![]()
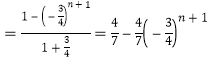
![]() .
.
注:因該隊這一賽季的全部比賽場次數(shù)為S , 則關(guān)系式![]() 只有在
只有在![]() 的情況下才成立.因為這一關(guān)系式所反映的獲得
的情況下才成立.因為這一關(guān)系式所反映的獲得![]() 分的概率是通過所有各種情況獲得
分的概率是通過所有各種情況獲得![]() 分的概率的總和, 即通過1 場比賽獲得
分的概率的總和, 即通過1 場比賽獲得![]() 分, 通過2場比賽獲得
分, 通過2場比賽獲得![]() 分, … …的概率之和, 其中, 也包括通過
分, … …的概率之和, 其中, 也包括通過![]() 場比賽獲得
場比賽獲得![]() 分的概率.
分的概率.
若![]() ,則因只限于
,則因只限于![]() 場比賽,應(yīng)該從中排除多于
場比賽,應(yīng)該從中排除多于![]() 場比賽獲得
場比賽獲得![]() 分的各種情況.所以,上述關(guān)系式已不再反映真實的獲得
分的各種情況.所以,上述關(guān)系式已不再反映真實的獲得![]() 分的概率.因此,只有在條件
分的概率.因此,只有在條件![]() 的情況下,由上述關(guān)系式計算的獲
的情況下,由上述關(guān)系式計算的獲![]() 分的概率才是正確的.
分的概率才是正確的.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】用水清洗一份蔬菜上殘留的農(nóng)藥,對用一定量的水清洗一次的效果作如下假定:用1個單位量的水可洗掉蔬菜上殘留農(nóng)藥量的![]() ,用水越多洗掉的農(nóng)藥量也越多,但總還有農(nóng)藥殘留在蔬菜上.設(shè)用
,用水越多洗掉的農(nóng)藥量也越多,但總還有農(nóng)藥殘留在蔬菜上.設(shè)用![]() 單位量的水清洗一次以后,蔬菜上殘留的農(nóng)藥量與本次清洗前殘留的農(nóng)藥量之比為函數(shù)
單位量的水清洗一次以后,蔬菜上殘留的農(nóng)藥量與本次清洗前殘留的農(nóng)藥量之比為函數(shù)![]() .
.
(1)求![]() 的值,并解釋其實際意義;
的值,并解釋其實際意義;
(2)現(xiàn)有![]() 單位量的水,可以清洗一次,也可以把水平均分成2份后清洗兩次,試問用哪種方案清洗后蔬菜上殘留的農(nóng)藥量比較少?說明理由.
單位量的水,可以清洗一次,也可以把水平均分成2份后清洗兩次,試問用哪種方案清洗后蔬菜上殘留的農(nóng)藥量比較少?說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 年
年![]() 月以來,湖北省武漢市持續(xù)開展流感及相關(guān)疾病監(jiān)測,發(fā)現(xiàn)多起病毒性肺炎病例,均診斷為病毒性肺炎肺部感染,后被命名為新型冠狀病毒肺炎(CoronaVirusDisease2019,COVID-19),簡稱“新冠肺炎”,下圖是
月以來,湖北省武漢市持續(xù)開展流感及相關(guān)疾病監(jiān)測,發(fā)現(xiàn)多起病毒性肺炎病例,均診斷為病毒性肺炎肺部感染,后被命名為新型冠狀病毒肺炎(CoronaVirusDisease2019,COVID-19),簡稱“新冠肺炎”,下圖是![]() 年
年![]() 月
月![]() 日至
日至![]() 月
月![]() 日累計確診人數(shù)隨時間變化的散點圖.
日累計確診人數(shù)隨時間變化的散點圖.

為了預(yù)測在未采取強力措施下,后期的累計確診人數(shù),建立了累計確診人數(shù)![]() 與時間變量
與時間變量![]() 的兩個回歸模型,根據(jù)
的兩個回歸模型,根據(jù)![]() 月
月![]() 日至
日至![]() 月
月![]() 日的數(shù)據(jù)(時間變量
日的數(shù)據(jù)(時間變量![]() 的值依次
的值依次![]() ,
,![]() ,…,
,…,![]() )建立模型
)建立模型![]() 和
和![]() .
.
參考數(shù)據(jù):其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據(jù)散點圖判斷,![]() 和
和![]() 哪一個適宜作為累計確診人數(shù)
哪一個適宜作為累計確診人數(shù)![]() 與時間變量
與時間變量![]() 的回歸方程類型?(給出判斷即可,不必說明理由);
的回歸方程類型?(給出判斷即可,不必說明理由);
(2)根據(jù)(1)的判斷結(jié)果及附表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(3)以下是![]() 月
月![]() 日至
日至![]() 月
月![]() 日累計確診人數(shù)的真實數(shù)據(jù),根據(jù)(2)的結(jié)果回答下列問題:
日累計確診人數(shù)的真實數(shù)據(jù),根據(jù)(2)的結(jié)果回答下列問題:
時間 |
|
|
|
|
|
累計確診人數(shù)的真實數(shù)據(jù) |
|
|
|
|
|
(i)當(dāng)![]() 月
月![]() 日至
日至![]() 月
月![]() 日這
日這![]() 天的誤差(模型預(yù)測數(shù)據(jù)與真實數(shù)據(jù)差值的絕對值與真實數(shù)據(jù)的比值)都小于
天的誤差(模型預(yù)測數(shù)據(jù)與真實數(shù)據(jù)差值的絕對值與真實數(shù)據(jù)的比值)都小于![]() 則認為模型可靠,請判斷(2)的回歸方程是否可靠?
則認為模型可靠,請判斷(2)的回歸方程是否可靠?
(ii)![]() 年
年![]() 月
月![]() 日在人民政府的強力領(lǐng)導(dǎo)下,全國人民共同取了強力的預(yù)防“新冠肺炎”的措施,若采取措施
日在人民政府的強力領(lǐng)導(dǎo)下,全國人民共同取了強力的預(yù)防“新冠肺炎”的措施,若采取措施![]() 天后,真實數(shù)據(jù)明顯低于預(yù)測數(shù)據(jù),則認為防護措施有效,請判斷預(yù)防措施是否有效?并說明理由.
天后,真實數(shù)據(jù)明顯低于預(yù)測數(shù)據(jù),則認為防護措施有效,請判斷預(yù)防措施是否有效?并說明理由.
附:對于一組數(shù)據(jù)![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 年
年![]() 月
月![]() 日,某市物價部門對本市的
日,某市物價部門對本市的![]() 家商場的某商品的一天銷售量及其價格進行調(diào)查,
家商場的某商品的一天銷售量及其價格進行調(diào)查,![]() 家商場的售價
家商場的售價![]() 元和銷售量
元和銷售量![]() 件之間的一組數(shù)據(jù)如表所示:
件之間的一組數(shù)據(jù)如表所示:
價格 | 9 | 9.5 | 10 | 10.5 | 11 |
銷售量 | 11 | 10 | 8 | 6 | 5 |
根據(jù)公式計算得相關(guān)系數(shù)![]() ,其線性回歸直線方程是:
,其線性回歸直線方程是:![]() ,則下列說法正確的有( )
,則下列說法正確的有( )
參考:![]()
A.有![]() 的把握認為變量
的把握認為變量![]() 具有線性相關(guān)關(guān)系
具有線性相關(guān)關(guān)系
B.回歸直線恒過定點![]()
C.![]()
D.當(dāng)![]() 時,
時,![]() 的估計值為
的估計值為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義域為[0,1])的函數(shù)f(x),如果同時滿足以下三條:①對任意的x∈[0,1],總有f(x)≥0;②f (1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立,則稱函數(shù)f(x)為理想函數(shù).
(1)判斷函數(shù)g(x)=2x﹣1(x∈[0,1])是否為理想函數(shù),并予以證明;
(2)若函數(shù)f(x)為理想函數(shù),假定存在x0∈[0,1],使得f(x0)∈[0,1],且f(f(x0))=x0,求證f(x0)=x0.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 對任意
對任意![]() 、
、![]() 都有
都有![]() ,且當(dāng)
,且當(dāng)![]() 時,
時,![]() .
.
(1)證明![]() 為奇函數(shù);
為奇函數(shù);
(2)證明![]() 在R上是減函數(shù);
在R上是減函數(shù);
(3)若![]() ,求
,求![]() 在區(qū)間
在區(qū)間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 與
與![]() 的圖象的交點個數(shù).
的圖象的交點個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“互聯(lián)網(wǎng)![]() ”是“智慧城市”的重要內(nèi)士,
”是“智慧城市”的重要內(nèi)士,![]() 市在智慧城市的建設(shè)中,為方便市民使用互聯(lián)網(wǎng),在主城區(qū)覆蓋了免費
市在智慧城市的建設(shè)中,為方便市民使用互聯(lián)網(wǎng),在主城區(qū)覆蓋了免費![]() .為了解免費
.為了解免費![]() 在
在![]() 市的使用情況,調(diào)査機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)査的網(wǎng)友中抽取了
市的使用情況,調(diào)査機構(gòu)借助網(wǎng)絡(luò)進行了問卷調(diào)查,并從參與調(diào)査的網(wǎng)友中抽取了![]() 人進行抽樣分析,得到如下列聯(lián)表(單位:人):
人進行抽樣分析,得到如下列聯(lián)表(單位:人):
經(jīng)常使用免費WiFi | 偶爾或不用免費WiFi | 合計 | |
45歲及以下 | 70 | 30 | 100 |
45歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據(jù)以上數(shù)據(jù),判斷是否有![]() 的把握認為
的把握認為![]() 市使用免費
市使用免費![]() 的情況與年齡有關(guān);
的情況與年齡有關(guān);
(2)將頻率視為概率,現(xiàn)從該市![]() 歲以上的市民中用隨機抽樣的方法每次抽取
歲以上的市民中用隨機抽樣的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.記被抽取的
次.記被抽取的![]() 人中“偶爾或不用免費
人中“偶爾或不用免費![]() ”的人數(shù)為
”的人數(shù)為![]() ,若每次抽取的結(jié)果是相互獨立的,求
,若每次抽取的結(jié)果是相互獨立的,求![]() 的分布列,數(shù)學(xué)期望
的分布列,數(shù)學(xué)期望![]() 和方差
和方差![]() .
.
附: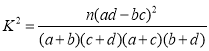 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com