
已知橢圓 的方程為
的方程為 ,其中
,其中 .
.
(1)求橢圓 形狀最圓時的方程;
形狀最圓時的方程;
(2)若橢圓 最圓時任意兩條互相垂直的切線相交于點
最圓時任意兩條互相垂直的切線相交于點 ,證明:點
,證明:點 在一個定圓上.
在一個定圓上.
(1) ;(2)證明過程詳見解析.
;(2)證明過程詳見解析.
【解析】
試題分析:本題主要考查橢圓的標準方程及其幾何性質、韋達定理等基礎知識,考查學生的分析問題解決問題的能力、轉化能力和計算能力.第一問,根據橢圓的標準方程應滿足的條件得: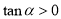 ,且
,且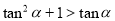 ,則知橢圓的長軸在y軸上,而橢圓形狀最圓時e最小,則先得到e的表達式,再根據三角函數的有界性求表達式的最小值,得到取得最小值時的
,則知橢圓的長軸在y軸上,而橢圓形狀最圓時e最小,則先得到e的表達式,再根據三角函數的有界性求表達式的最小值,得到取得最小值時的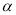 的值,從而得到橢圓的標準方程;第二問,設出交點P的坐標,根據直線的斜率是否存在,分2種情況討論,當斜率存在時,設出直線方程,與橢圓方程聯立,得到關于k的方程,由于兩切線垂直,則
的值,從而得到橢圓的標準方程;第二問,設出交點P的坐標,根據直線的斜率是否存在,分2種情況討論,當斜率存在時,設出直線方程,與橢圓方程聯立,得到關于k的方程,由于兩切線垂直,則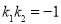 ,利用上述方程的兩根之積得到
,利用上述方程的兩根之積得到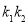 的值,整理出方程形式,再驗證當斜率不存在時P點坐標,得到最終結論.
的值,整理出方程形式,再驗證當斜率不存在時P點坐標,得到最終結論.
試題解析:(1)根據已知條件有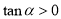 ,且
,且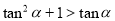 ,故橢圓
,故橢圓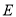 的長軸在
的長軸在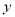 軸上.
軸上.
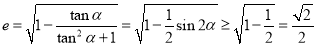 ,當且僅當
,當且僅當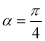 時取等號.
時取等號.
由于橢圓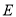 的離心率
的離心率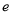 最小時其形狀最圓,故最圓的橢圓方程為
最小時其形狀最圓,故最圓的橢圓方程為 . 5分
. 5分
(2)設交點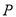
 ,過交點
,過交點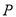 的直線
的直線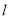 與橢圓
與橢圓 相切.
相切.
(1)當斜率不存在或等于零時,易得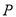 點的坐標為
點的坐標為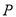
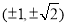 . 6分
. 6分
(2)當斜率存在且非零時,則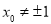 設斜率為
設斜率為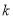 ,則直線
,則直線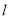 :
: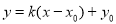 ,
,
與橢圓方程聯立消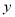 ,得:
,得: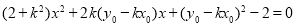 .
.
由相切,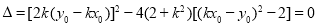 ,
,
化簡整理得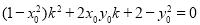 .①
.①
因過橢圓外一點有兩條直線與橢圓相切,由已知兩切線垂直,故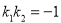 ,而
,而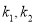 為方程①的兩根,
為方程①的兩根,
故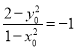 ,整理得:
,整理得: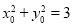 .
.
又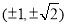 也滿足上式,
也滿足上式,
故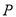 點的軌跡方程為
點的軌跡方程為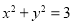 ,即
,即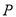 點在定圓
點在定圓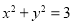 上. 13分
上. 13分
考點:橢圓的標準方程及其幾何性質、韋達定理.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試理科數學試卷(解析版) 題型:選擇題
已知 ,函數
,函數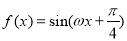 在
在 上單調遞減.則
上單調遞減.則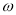 的取值范圍是 ( )
的取值范圍是 ( )
A.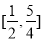 B.
B.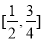 C.
C.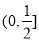 D.
D.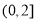
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省皖北協作區高三年級聯考文科數學試卷(解析版) 題型:填空題
某公司為改善職工的出行條件,隨機抽取50名職工,調查他們的居住地與公司的距離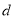 [單位:千米].若樣本數據分組為
[單位:千米].若樣本數據分組為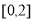 ,
, 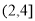 ,
,  ,
, 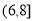 ,
, 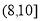 ,
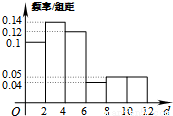
, 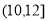 , 有數據繪制的頻率分布直方圖如圖所示,則樣本中職工居住地與公司的距離不超過4千米的人數為__________.
, 有數據繪制的頻率分布直方圖如圖所示,則樣本中職工居住地與公司的距離不超過4千米的人數為__________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省安慶市高三第二次模擬考試理科數學試卷(解析版) 題型:填空題
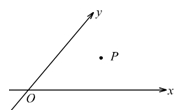
如圖,設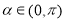 ,且
,且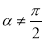 .當
.當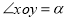 時,定義平面坐標系
時,定義平面坐標系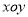 為
為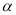 -仿射坐標系,在
-仿射坐標系,在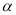 -仿射坐標系中,任意一點
-仿射坐標系中,任意一點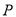 的斜坐標這樣定義:
的斜坐標這樣定義: 分別為與
分別為與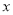 軸、
軸、 軸正向相同的單位向量,若
軸正向相同的單位向量,若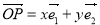 ,則記為
,則記為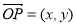 ,那么在以下的結論中,正確的有.(填上所有正確結論的序號)
,那么在以下的結論中,正確的有.(填上所有正確結論的序號)
①設 、
、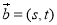 ,若
,若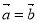 ,則
,則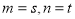 ;
;
②設 ,則
,則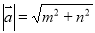 ;
;
③設 、
、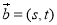 ,若
,若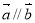 ,則
,則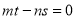 ;
;
④設 、
、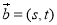 ,若
,若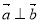 ,則
,則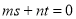 ;
;
⑤設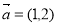 、
、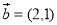 ,若
,若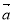 與
與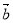 的夾角
的夾角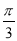 ,則
,則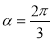 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省安慶市高三第二次模擬考試理科數學試卷(解析版) 題型:選擇題
數列 共有5項,其中
共有5項,其中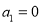 ,
, ,且
,且 ,
, ,則滿足條件的不同數列的個數為( )
,則滿足條件的不同數列的個數為( )
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省安慶市高三第二次模擬考試文科數學試卷(解析版) 題型:填空題
已知點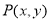 滿足約束條件
滿足約束條件 ,
, 為坐標原點,則
為坐標原點,則 的最大值為_______________.
的最大值為_______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com